SOLVING QUADRATIC EQUATIONS BY EXTRACTING SQUARE ROOTS || GRADE 9 MATHEMATICS Q1
Summary
TLDRThis educational video explains how to solve quadratic equations by extracting square roots. It covers perfect square numbers like 1, 4, 9, and 49, and demonstrates solving equations such as x^2 = 49 and x^2 = 169. The video also addresses non-perfect square numbers, showing how to handle equations like x^2 = 75 and x^2 = 80 by factoring. Additionally, it includes examples of more complex equations involving quantities, teaching viewers to simplify and solve for x. The tutorial is designed to help students understand and apply these mathematical concepts effectively.
Takeaways
- 📚 The video introduces the concept of perfect squares and their significance in solving quadratic equations.
- 🔍 It demonstrates how to solve quadratic equations by extracting square roots, particularly when the equation is a perfect square.
- 📐 The script provides a step-by-step method for extracting square roots, starting with taking the square root of both sides of the equation.
- 🔢 Examples are given to illustrate the process, including the solution for equations where the result is a perfect square, such as x^2 = 49 leading to x = ±7.
- 🎓 The video explains how to handle non-perfect square numbers by factoring them into a product of a perfect square and another factor.
- 📉 For non-perfect squares, the script shows the process of isolating the perfect square part and then extracting its square root.
- 📝 The transcript includes solving quadratic equations with coefficients and constants, such as 2(5x + 2)^2 = 64, by simplifying and applying the square root.
- 🤔 It addresses the complexity of solving equations where the squared term is not a perfect square, by finding factors that simplify the equation.
- 📈 The video script shows how to deal with equations that require dividing by a coefficient before applying the square root.
- 📚 It concludes with solving more complex equations that involve multiple steps, such as dividing and then taking the square root.
- 👍 The video encourages viewers to like, subscribe, and hit the bell button for more educational content.
Q & A
What is the main topic of the video?
-The main topic of the video is solving quadratic equations by extracting square roots and understanding perfect squares.
What are perfect squares?
-Perfect squares are numbers that are the product of an integer multiplied by itself, such as 1, 4, 9, 16, 25, 36, etc.
How does the video demonstrate solving a quadratic equation when the given number is a perfect square?
-The video demonstrates by taking the square root of both sides of the equation, simplifying to find x equals to the square root of the perfect square number, considering both positive and negative roots.
What is the process for solving a quadratic equation when the given number is not a perfect square?
-The process involves taking the square root of both sides, finding factors of the given number that include a perfect square, and then simplifying to solve for x, considering both positive and negative roots.
In the video, how is the quadratic equation x^2 = 75 solved?
-The equation is solved by taking the square root of both sides, factoring 75 into 25 * 3, and then simplifying to x = ±√(25 * 3), which further simplifies to x = ±5√3.
What is the solution for the quadratic equation 2(x - 5)^2 = 32 in the video?
-The solution is found by dividing both sides by 2, taking the square root of both sides, and solving for x, which results in two solutions: x = 9 and x = 1.
How does the video handle the quadratic equation 3(4x - 1)^2 - 1 = 11?
-The video adds 1 to both sides to make it 3(4x - 1)^2 = 12, divides by 3, and then takes the square root of both sides to solve for x, resulting in two solutions: x = 3/4 and x = -1/4.
What is the significance of dividing both sides by 2 in the equation 2(5x + 2)^2 = 64?
-Dividing both sides by 2 simplifies the equation to (5x + 2)^2 = 32, making it easier to take the square root of both sides and solve for x.
How are the solutions for the equation (2x - 3)^2 = 18 derived in the video?
-The video takes the square root of both sides, resulting in 2x - 3 = ±3√2, and then solves for x, yielding two solutions: x = (3 + 3√2)/2 and x = (3 - 3√2)/2.
What is the final example given in the video, and what are its solutions?
-The final example is 2(5x + 2)^2 = 64, and its solutions are x = (-2 + 4√2)/5 and x = (-2 - 4√2)/5 after simplifying and solving for x.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

How to Solve Quadratic Equations by Extracting the Square Root? @MathTeacherGon

SOLVING QUADRATIC EQUATIONS BY COMPLETING THE SQUARE || GRADE 9 MATHEMATICS Q1
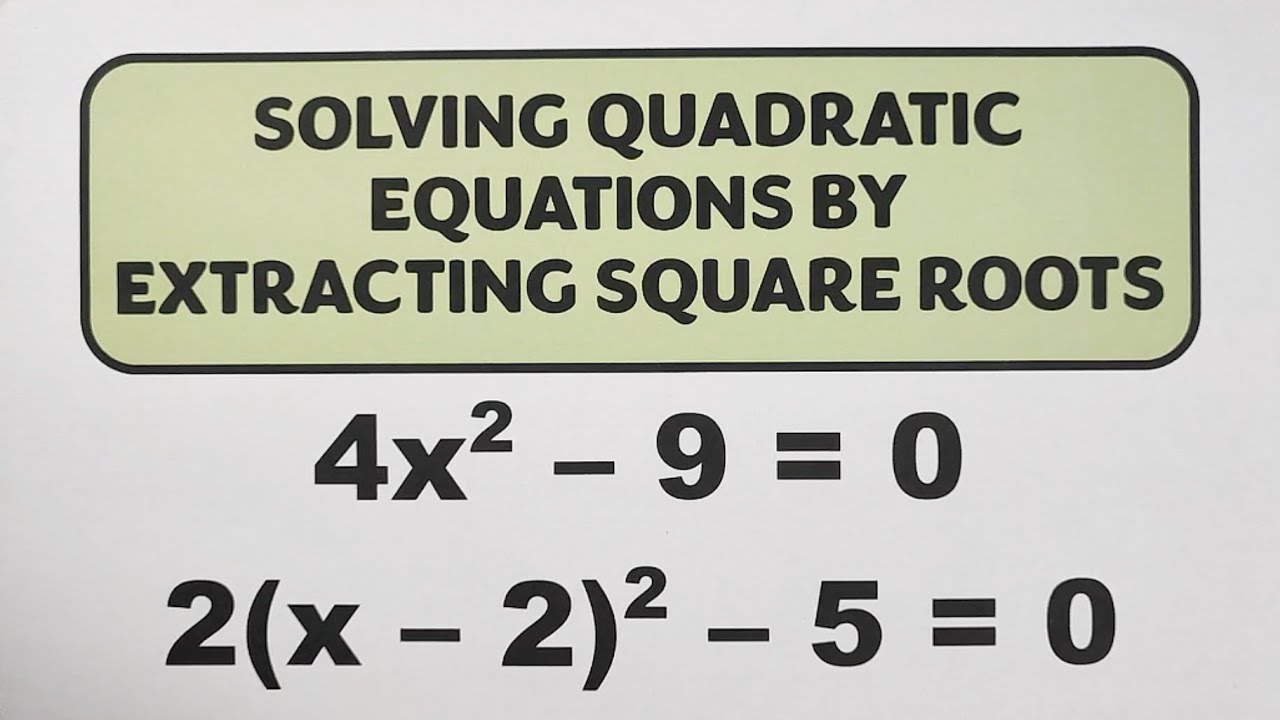
Solving Quadratic Equations by Extracting the Square Roots by @MathTeacherGon

How to Solve These Quadratic Equations?

SOLVING QUADRATIC EQUATIONS USING QUADRATIC FORMULA | Grade 9 Learning Task 3 Week 1

PERSAMAAN KUADRAT part ZERO-ONE
5.0 / 5 (0 votes)