Lecture Part 4 Video 3 Topic 18

Summary

This video script delves into the concepts of intersections and unions in probability, crucial for calculating the likelihood of multiple characteristics. It emphasizes the significance of the conjunction 'and' for intersections, focusing on overlapping outcomes, and 'or' for unions, necessitating careful counting to avoid double-counting. The script illustrates these principles with examples, such as rolling a die and analyzing a contingency table, to clarify how to compute probabilities accurately without overcounting shared events.

Takeaways

• 📚 When calculating probabilities, focus on the conjunctions 'and' and 'or' as they determine whether you're looking for intersections or unions of events.
• 🔍 For intersections ('and' scenarios), count the overlap between two events, ensuring the outcomes have both characteristics of interest.
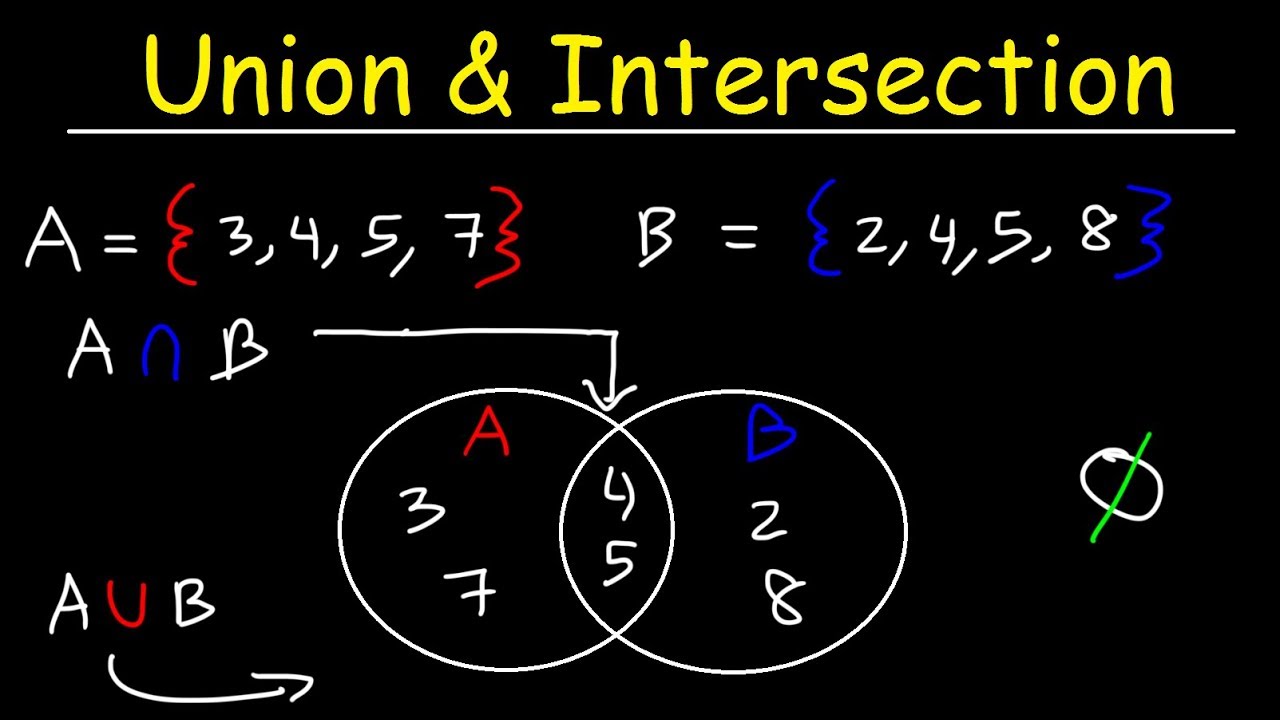
• 📈 The formula for intersection probability is (Number of A and B) / Total Possible Outcomes, where A and B are the events of interest.
• 🚫 Be cautious with unions ('or' scenarios) to avoid double counting by subtracting the intersection of events from the total count.
• 🧮 The union probability formula is (Number of A) + (Number of B) - (Number of A and B) / Total Possible Outcomes.
• 📊 Contingency tables are useful for visualizing and calculating probabilities, especially for intersections and unions within categorical data.
• 🎯 Remember, the denominator for both intersections and unions is the total number of possible outcomes, not just the outcomes within the events.
• 📝 When using a contingency table, the intersection probability is found in the cell that corresponds to both the row and column of interest.
• 🤝 Alternatively, you can calculate the probabilities of individual events and their intersection, then use those to find the union probability.
• 💡 Always double-check your work, especially when dealing with unions, to ensure you haven't overcounted any outcomes.

Q & A

What is the key difference between calculating probabilities for intersections and unions?

The key difference lies in the use of the words 'and' for intersections and 'or' for unions. Intersections require finding the overlap or common outcomes of two events (A and B), while unions involve careful counting to include outcomes from either event A or B without double-counting the overlap.

Why is it important to subtract the intersection when calculating the union of two events?

Subtracting the intersection is crucial when calculating the union to avoid double-counting outcomes that belong to both events. Without this subtraction, the numerator would be inflated, leading to an incorrect probability calculation.

What is the significance of the word 'and' in probability problems involving two characteristics?

The word 'and' signifies that you are interested in the probability of both characteristics occurring together. This focuses on the outcomes that have both of the specified characteristics, which is the intersection of the two events.

How does the use of the word 'or' change the probability calculation compared to 'and'?

Using 'or' changes the calculation to a union, where you are interested in the probability of either one or both characteristics occurring. This requires adding the probabilities of each event and then subtracting the probability of their intersection to avoid counting outcomes that are in both events twice.

What is the formula for calculating the union of two events, and why is it necessary?

The formula for the union of two events is P(A or B) = P(A) + P(B) - P(A and B). It is necessary to subtract P(A and B) to correct for the double-counting that would occur if you simply added P(A) and P(B).

Can you provide an example from the script where the concept of intersection is applied?

Yes, an example is given with a fair six-sided die where the probability of rolling an even number (2, 4, 6) and a number greater than two is calculated. The intersection of these two events is the numbers 4 and 6, which are both even and greater than two.

How does the script handle the calculation of probabilities using a contingency table?

The script demonstrates the use of a contingency table by identifying the intersection or union within the table. For intersections, it focuses on the cell that represents both characteristics of interest. For unions, it sums the counts from the relevant row and column, but subtracts the intersection to avoid overcounting.

What is the mistake often made when calculating the union of two events from a contingency table?

The common mistake is adding the totals of the row and column without subtracting the count of the intersection, which leads to overcounting and an incorrect probability.

Why is it essential to carefully count when calculating the union of two events?

Careful counting is essential to ensure that outcomes are not counted more than once, which would result in an inflated numerator and an incorrect probability. This is particularly important when dealing with overlapping events.

How does the script suggest using previously calculated probabilities to find the union of two events?

The script suggests using the probabilities of each event individually (P(A) and P(B)) and the probability of their intersection (P(A and B)) to calculate the union without having to refer back to the contingency table. This method simplifies the process when the individual probabilities are already known.