AP Precalculus – 1.2 Rates of Change
Summary
TLDRThis educational video script covers the concept of rates of change, focusing on average rate of change and slope. It explains the use of the Greek letter Delta to denote change and the formula for calculating the average rate of change between two points. The script includes examples using both a graph and a table of values to demonstrate how to find the average rate of change. It also explores estimating the rate of change at a single point by using very small intervals and discusses the implications of positive and negative rates of change, illustrating these concepts with the help of a graphing calculator and practical examples.
Takeaways
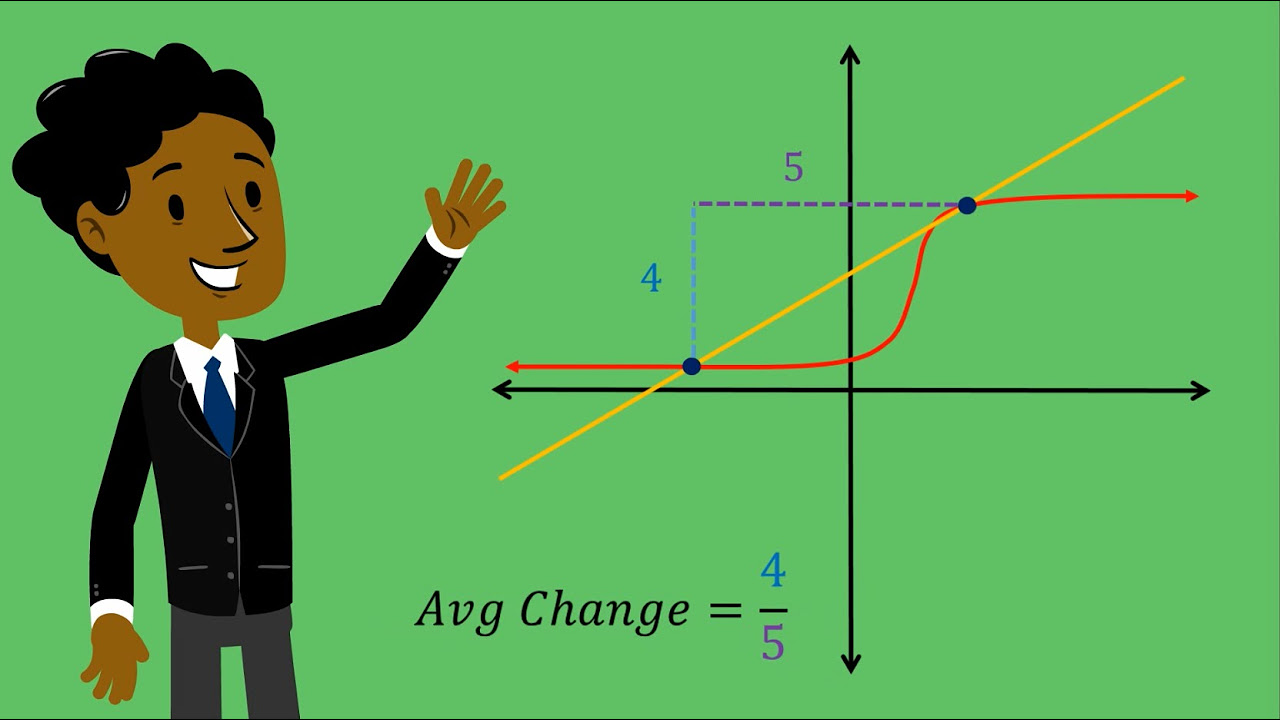
- 📈 The concept of 'average rate of change' is introduced, which is calculated as the change in the dependent variable (Δy) over the change in the independent variable (Δx), analogous to the idea of slope from previous math studies.
- 🔄 The Greek letter 'Delta' (Δ) is used to denote 'change in', simplifying the expression of the rate of change.
- ✏️ It's emphasized that the dependent variable should always be on top in the rate of change formula (Δy / Δx).
- 🔢 The script demonstrates how to calculate the average rate of change between two points on a graph by finding the slope of the line that connects them.
- 🤔 A 'what if' scenario is explored to show that the order of points in the rate of change formula doesn't affect the result due to the nature of subtraction.
- 📊 The script explains how to use a table of values to calculate the average rate of change over an interval, highlighting the importance of matching the correct x and y values.
- 📉 The importance of units in rate of change is underlined, showing how it indicates the relationship between quantities, such as 'meters per second'.
- 📍 The script discusses estimating the rate of change at a single point by using very small intervals around that point, illustrating this with a graphing tool.
- 📱 The use of a calculator to find the rate of change for closely spaced points is demonstrated, showing how to input functions and use the table feature for precise calculations.
- ↗️ Positive and negative rates of change are explained in terms of how one quantity's increase or decrease affects the other, with positive rates indicating同步 increase or decrease, and negative rates indicating opposite changes.
Q & A
What is the average rate of change and how is it calculated?
-The average rate of change is a measure of how a dependent variable changes for every change in the independent variable. It is calculated using the formula Δy/Δx, where Δy is the change in the dependent variable (y2 - y1) and Δx is the change in the independent variable (x2 - x1).
What does the Greek letter Delta represent in the context of rates of change?
-In the context of rates of change, the Greek letter Delta (Δ) represents the change in a variable. It is used to denote the difference between two values of a variable, such as Δy for the change in y and Δx for the change in x.
Why is it important to have the dependent variable on top when calculating the average rate of change?
-It is important to have the dependent variable on top when calculating the average rate of change to maintain consistency in the formula Δy/Δx. This ensures that the rate of change is expressed as a ratio of the change in the dependent variable over the change in the independent variable.
What is the significance of the 'per' in rates of change, such as miles per hour?
-The 'per' in rates of change signifies the unit of the dependent variable per unit of the independent variable. For example, in miles per hour, it indicates the distance traveled (dependent variable) per unit of time (independent variable).
How can you estimate the rate of change at a single point using a graph?
-To estimate the rate of change at a single point using a graph, you can use the average rate of change over very small intervals that contain the point. As the intervals become smaller and the points get closer together, the line connecting these points approximates the tangent line at that point, giving a more accurate estimate of the rate of change.
What is the purpose of using a table of values to calculate the average rate of change?
-A table of values is used to calculate the average rate of change to provide a systematic way of determining the changes in variables over a specific interval. It allows for the easy identification of corresponding x and y values, which can then be used in the rate of change formula.
Why is it necessary to include units when calculating rates of change?
-Including units when calculating rates of change is necessary to ensure that the result is meaningful and provides context to the rate. It indicates the relationship between the units of the dependent and independent variables, making the rate of change a dimensional quantity that can be interpreted correctly.
How can you find the average rate of change using a calculator?
-To find the average rate of change using a calculator, you can input the function into the calculator's function notation and then use the table feature to generate values for different x inputs. You can then manually calculate the average rate of change by finding the difference in y values divided by the difference in x values.
What is the difference between a positive and a negative rate of change?
-A positive rate of change indicates that as one quantity increases, the other quantity also increases, while a negative rate of change indicates that as one quantity increases, the other quantity decreases. This can be visualized on a graph as moving uphill (positive) or downhill (negative) from left to right.
How can you determine whether a given rate of change is positive or negative based on a real-world scenario?
-To determine whether a given rate of change is positive or negative based on a real-world scenario, you can consider how the quantities change in relation to each other. If they change in the same direction (both increase or both decrease), the rate of change is positive. If they change in opposite directions, the rate of change is negative.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenant5.0 / 5 (0 votes)