Intersecciones de una función con los ejes X e Y / Función Lineal

Summary

Este video educativo se centra en el análisis de las intersecciones de funciones con los ejes del plano cartesiano. Se explica que estas intersecciones son puntos específicos donde la función toca los ejes X o Y. Se utilizan funciones lineales como ejemplo para demostrar cómo calcular estas intersecciones, destacando que para encontrar la intersección con el eje Y, el valor de X se establece en cero, y viceversa. Se proporcionan pasos detallados para resolver ecuaciones y encontrar coordenadas de intersección, subrayando la importancia de comprender estos conceptos para realizar cálculos algebraicos en futuras lecciones.

Takeaways

• 😀 La intersección de una función con los ejes del plano cartesiano se refiere a los puntos específicos donde la función corta los ejes X e Y.
• 📏 Cuando una función intersecta con el eje X, el valor de Y siempre será 0, y viceversa para el eje Y.
• 📈 Las intersecciones con los ejes son importantes para realizar cálculos algebraicos de intersecciones sin utilizar gráficas.
• 🔢 Para encontrar la intersección con el eje Y, se establece la función igual a 0 y se resuelve para encontrar el valor de X.
• 🔄 Al calcular la intersección con el eje X, se establece Y igual a 0 en la función y se resuelve para encontrar el valor de Y.
• ✅ Las funciones lineales tienen una única intersección con cada eje, mientras que funciones de orden superior pueden tener múltiples intersecciones.
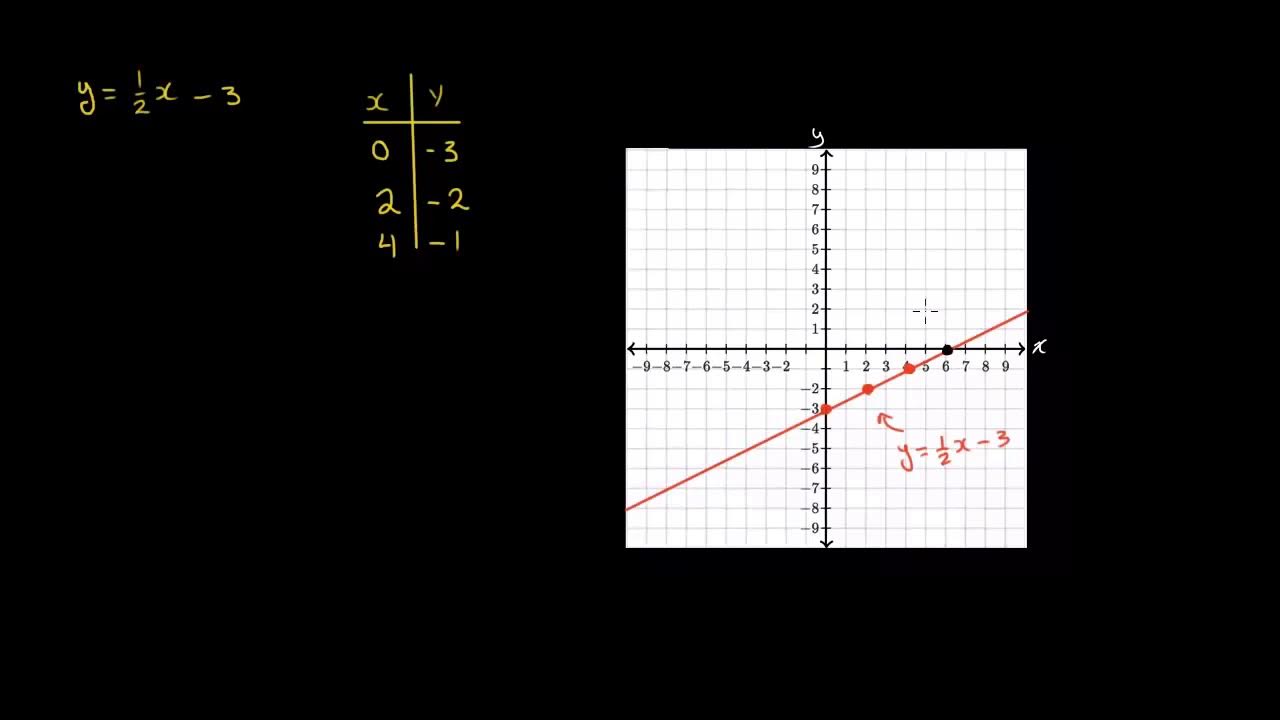
• 📉 En el ejemplo dado, la función 3x + 9 intersecta con el eje Y en la coordenada (0, 9) y con el eje X en la coordenada (-3, 0).
• 📊 Al simplificar funciones algebraicas, es posible identificar y calcular las intersecciones de manera más eficiente.
• 📐 La sustitución de valores en la función para encontrar intersecciones es un método directo y efectivo para resolver ecuaciones.
• 🎓 El análisis de intersecciones es una herramienta fundamental en el estudio de funciones y su comportamiento en el plano cartesiano.

Q & A

¿Qué son las intersecciones de una función con los ejes del plano cartesiano?

Las intersecciones de una función con los ejes del plano cartesiano son los puntos o coordenadas específicas por donde la función cruza los ejes X (horizontal) y Y (vertical).

Cuál es la particularidad de las intersecciones de una función con el eje X?

La particularidad de las intersecciones de una función con el eje X es que el valor de Y siempre será 0, ya que en estos puntos la función toca el eje X.

¿Cómo se calcula la intersección de una función con el eje Y?

Para calcular la intersección de una función con el eje Y, se establece que el valor de X es 0 y se resuelve la función para encontrar el valor correspondiente de Y.

¿Qué ocurre cuando una función intersecta con el eje X en una función lineal?

Cuando una función lineal intersecta con el eje X, existe una única intersección en la que el valor de Y es cero, y se determina el valor de X que satisface esta condición.

¿Cómo se determina la intersección de una función con el eje Y en una función lineal?

Para determinar la intersección de una función lineal con el eje Y, se establece que el valor de X es 0 y se evalúa la función para obtener el valor de Y en ese punto.

¿Qué es la despeja en el contexto de resolver ecuaciones para encontrar intersecciones?

La despeja es el proceso de aislar una variable en una ecuación para determinar su valor, lo cual es necesario para encontrar las intersecciones de una función con los ejes.

¿Por qué es importante saber si una función intersecta con el eje X o Y en el cálculo de intersecciones?

Es importante saber si una función intersecta con el eje X o Y porque esto nos da un punto de partida para resolver algebraicamente la ecuación y encontrar la intersección exacta.

¿Cómo se simplifica una función lineal antes de calcular sus intersecciones con los ejes?

Se simplifica una función lineal combinando términos similares y reduciendo la expresión al mínimo, lo que facilita el cálculo de intersecciones al tener una forma más manejable.

¿Cuáles son las diferencias entre las intersecciones de funciones lineales y cuadráticas con los ejes?

Las funciones lineales generalmente tienen una única intersección con cada eje, mientras que las funciones cuadráticas pueden tener hasta dos intersecciones con el eje X y ninguna o dos con el eje Y.

¿Cómo se verifican las intersecciones de una función con los ejes en una gráfica?

Se verifican las intersecciones de una función con los ejes en una gráfica observando los puntos en los que la curva de la función toca los ejes X y Y.