02 Hooke's Law
Summary
TLDR本视频脚本介绍了胡克定律,即弹簧的弹性行为。通过实验观察不同负载下弹簧的伸长情况,发现弹簧的伸长与施加的力成正比,这个比例常数被称为弹簧常数K。然而,当比较不同尺寸的弹簧时,会发现即使材料相同,它们的弹簧常数也不同,这引发了对材料力学性能更深入探讨的问题。视频以弹簧实验为引子,引导观众思考如何通过应力和应变来统一比较不同材料的力学行为。
Takeaways
- 📚 胡克定律是描述弹簧在受力时行为的基本法则。
- 🔍 当弹簧受到拉伸或压缩时,其长度会发生变化,这种变化称为伸长或压缩。
- 📏 弹簧的原始长度用L₀表示,伸长或压缩后的长度变化用ΔL或X表示。
- 📈 力与伸长之间的关系通常是线性的,这种线性关系的斜率称为弹簧常数(K)。
- 🧮 胡克定律的数学表达式为F = KX,其中F是作用力,X是伸长量,K是弹簧常数。
- 🔧 弹簧常数K是一个特定的值,它反映了弹簧材料的弹性特性。
- 📊 当比较不同弹簧时,如果它们由相同材料制成,但尺寸不同,它们的弹簧常数K会有所不同。
- 🔬 为了解决不同尺寸弹簧的比较问题,引入了应力和应变的概念。
- 🌐 应力是单位面积上的力,而应变是材料尺寸变化与原始尺寸的比率。
- 🔄 通过引入应力和应变,可以更公平地比较不同尺寸和形状的弹簧材料的机械行为。
Q & A
胡克定律是什么?
-胡克定律是描述弹性物体在受到外力作用时形变与作用力成正比关系的定律,通常表达为 F = kX,其中 F 是作用力,k 是弹簧常数,X 是物体的形变或伸长量。
什么是弹簧的原长?
-弹簧的原长,也称为休息长度,是指弹簧在没有受到外力作用时的自然长度,通常用 L₀ 表示。
弹簧的伸长量通常用什么字母表示?
-弹簧的伸长量通常用 ΔL 或 X 表示,它描述了弹簧在受到外力作用后相对于原长增加的长度。
如何得到弹簧的力与伸长量的关系图?
-通过对不同重量的负载施加在弹簧上并测量相应的伸长量,然后将这些数据点绘制在力与伸长量的坐标图上,可以得到一条直线,这条直线的斜率即为弹簧常数。
弹簧常数 K 代表什么?
-弹簧常数 K 代表弹簧的刚度,它是一个衡量弹簧抵抗形变能力的量,数值越大表示弹簧越硬,即需要更大的力才能产生相同的形变。
为什么不同尺寸的弹簧即使由相同材料制成,它们的弹簧常数也会不同?
-不同尺寸的弹簧即使由相同材料制成,它们的弹簧常数也会不同,因为弹簧的刚度不仅取决于材料,还受到弹簧的尺寸、形状和横截面积等因素的影响。
在比较两个不同尺寸的弹簧时,我们如何确定它们的材料属性是否相同?
-在比较两个不同尺寸的弹簧时,可以通过确保它们由相同材料制成,并且施加相同的力来观察它们的形变量,从而比较它们的材料属性。
为什么在胡克定律中,斜率 B 通常为零?
-在胡克定律中,斜率 B 通常为零是因为在理想情况下,弹簧在没有负载时不会自然伸长或压缩,因此当力为零时,伸长量也应为零,使得直线关系通过原点。
如果两个弹簧由不同材料制成,它们的力与伸长量关系会有什么不同?
-如果两个弹簧由不同材料制成,即使尺寸相同,它们的力与伸长量关系也会不同,因为不同材料的弹性模量和屈服强度不同,导致弹簧常数 K 有显著差异。
胡克定律在实际应用中有哪些局限性?
-胡克定律在实际应用中的局限性包括:只适用于弹性范围内的形变,对于超出弹性极限的塑性形变或断裂不适用;对于非线性材料,如橡胶等,胡克定律不适用;对于复杂形状或结构的物体,胡克定律可能需要进行修正或使用更复杂的模型。
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Stress Strain Curve | Mechanical Properties of Solids | AASOKA
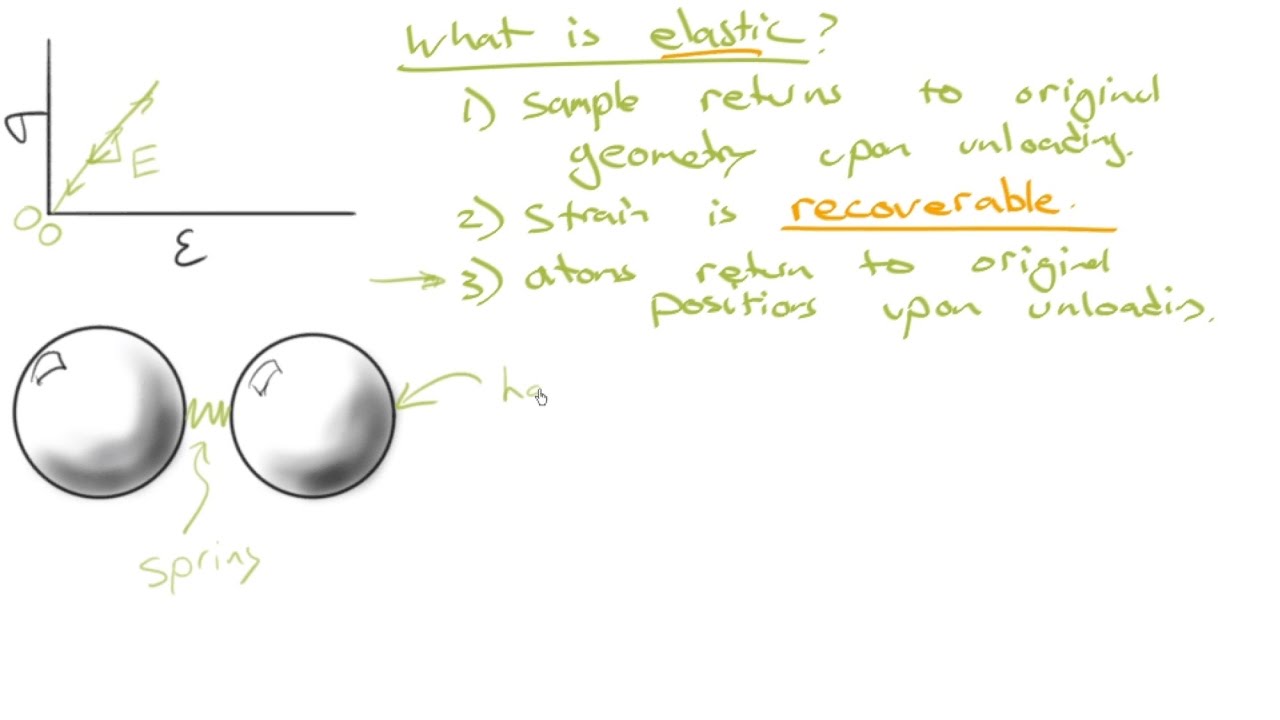
04 Atomic Definition of Young's Modulus

ATACM Long Range Missile is Unstoppable

How to create resizable sheets in SwiftUI | Bootcamp #64

Putin Targets CHILDREN'S CANCER HOSPITAL!

Finally! Putin Showed Off A New Terrifying Hypersonic Missile That Shocked NATO
5.0 / 5 (0 votes)
