Vector Calculus Module 4 Core Ideas
Summary
TLDRThe transcript introduces 15 core concepts of vector calculus, covering topics such as the differential operator (D), scalar fields, directional derivatives, solenoidal and irrotational fields, vector integration, surface and volume integrals, as well as the Divergence and Stokes' theorems. It provides definitions and formulae for gradients, curls, and integrals, along with how to apply them in different planes and dimensions. Additionally, it explains the significance of conservative force fields and scalar potentials. The focus is on understanding these concepts to solve related exercises efficiently.
Takeaways
- 📐 The vector differential operator D is defined as a combination of partial derivatives with respect to x, y, and z.
- 📊 If f is a differentiable scalar field, the gradient of f, denoted by Del, is a vector consisting of partial derivatives of f.
- 👉 The directional derivative of a scalar field in the direction of a unit vector a is calculated using the dot product of Del and vector a.
- 🔗 The unit normal vector to a level surface is derived from the gradient of the scalar field and is perpendicular to the surface.
- 🌐 Divergence of a vector field F is obtained by taking the dot product of Del with F, resulting in a scalar field. If this is zero, F is solenoidal.
- 🔄 Curl of a vector field F is determined by the cross product of Del with F. If the curl is zero, the vector field is irrotational and forms a conservative force field.
- 🔍 Surface integrals can be computed by projecting the surface onto a plane and integrating over the projected region, adjusting the formula based on the chosen plane.
- 📏 The Divergence Theorem allows surface integrals to be converted into volume integrals, simplifying the evaluation process.
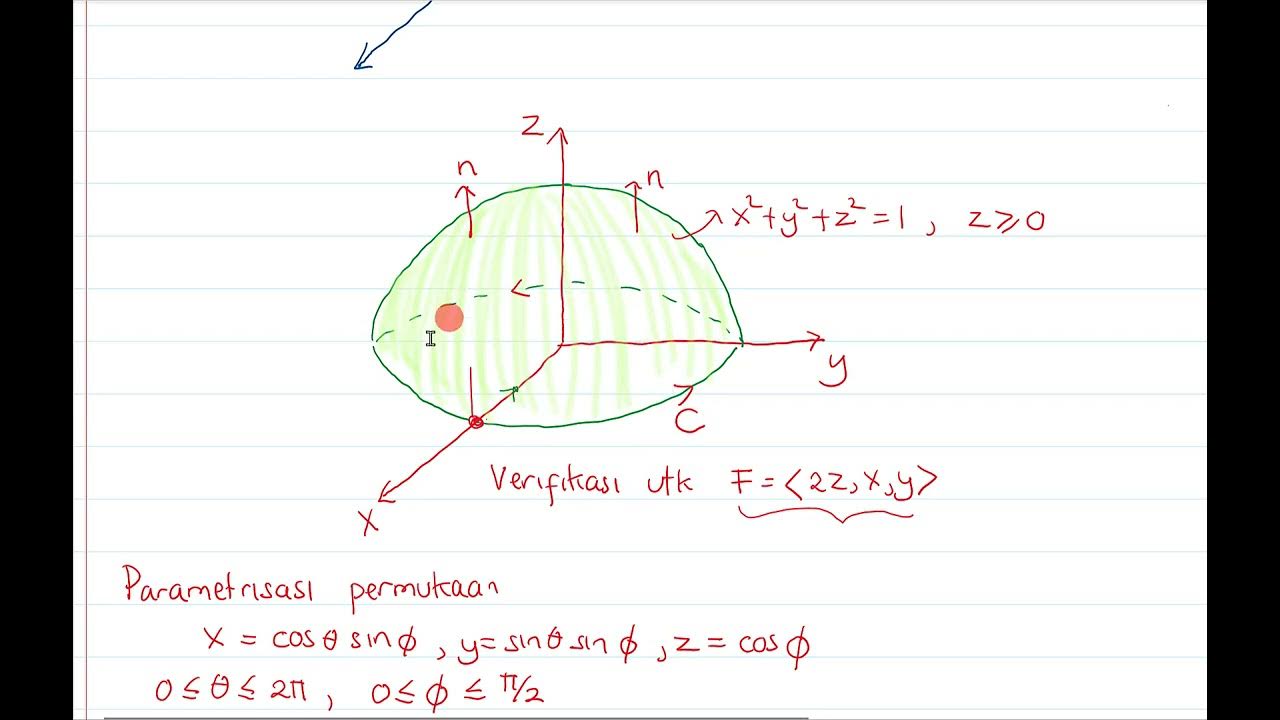
- ➰ Stokes' Theorem relates a surface integral to a line integral over the boundary curve, allowing for easier evaluation of certain integrals.
- ✏️ The 15 core concepts outlined in the script are crucial for understanding and applying vector calculus, especially in relation to gradients, divergence, curl, and various integral theorems.
Q & A
What is the vector differential operator?
-The vector differential operator is denoted by 'del' or 'D', and it is defined as the vector composed of the partial derivatives with respect to each spatial coordinate, represented as D = (∂/∂x)i + (∂/∂y)j + (∂/∂z)k.
What is the directional derivative of a scalar field F in the direction of a vector a?
-The directional derivative of a scalar field F in the direction of a vector a is given by the dot product of the gradient of F (denoted as 'Del F' or 'grad F') and the unit vector in the direction of a (denoted as 'a cap'), which is (Del F) dot a cap.
What is meant by the unit normal vector to the level surface of a scalar field?
-The unit normal vector to the level surface of a scalar field is the vector that is perpendicular to the level surface at a given point, and it is obtained by taking the gradient of the scalar field and normalizing it.
How is divergence defined and what does it represent?
-Divergence is defined as the dot product of the del operator with a vector field, mathematically represented as 'Del dot F'. It represents the rate at which the vector field spreads out or converges at a given point.
What is the condition for a vector field to be solenoidal?
-A vector field is solenoidal if its divergence is zero, i.e., 'Del dot F' = 0. This implies that the field has no sources or sinks.
How is the curl of a vector field calculated?
-The curl of a vector field F is calculated using the cross product of the del operator with the vector field, represented as 'Del cross F'. It is computed using a determinant involving the unit vectors i, j, k, and the partial derivatives of the components of the vector field.
What does it mean for a vector field to be irrotational?
-A vector field is irrotational if its curl is zero, i.e., 'Del cross F' = 0. This indicates that the field is the gradient of a scalar potential function.
What is the physical interpretation of the line integral of a vector field over a curve?
-The line integral of a vector field over a curve represents the work done by the force represented by the vector field along the path of the curve.
How is a surface integral evaluated?
-A surface integral is evaluated by projecting the surface onto a plane, determining the projection region, and then integrating the dot product of the vector field with the unit normal vector over the projection region.
What is the divergence theorem and how is it applied?
-The divergence theorem states that the surface integral of a vector field over a closed surface is equal to the triple integral of the divergence of the vector field over the volume enclosed by the surface. It allows the evaluation of a surface integral in terms of a volume integral.
What does Stokes' theorem state and how is it used?
-Stokes' theorem states that the surface integral of the curl of a vector field over a surface is equal to the line integral of the vector field around the boundary of the surface. It is used to evaluate a surface integral using a line integral, particularly for closed curves.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Concept of Vector Point Function & Vector Differentiation By GP Sir

Div, Grad, and Curl: Vector Calculus Building Blocks for PDEs [Divergence, Gradient, and Curl]

This Downward Pointing Triangle Means Grad Div and Curl in Vector Calculus (Nabla / Del) by Parth G

calc 3 vector fields

M172 - Operator Diferensial Vektor : Del atau Nabla,memahami secara mudah
Teorema Stokes1
5.0 / 5 (0 votes)
