Concept of Vector Point Function & Vector Differentiation By GP Sir
Summary
TLDRThis video offers an insightful exploration of vector calculus, focusing on vector differentiation and integration. The instructor explains the fundamental concepts of vectors, including their directional components and differentiation using the 'del' operator. Key topics covered include the gradient, divergence, and curl, with practical applications such as finding normal vectors, unit normal vectors, and directional derivatives. The video also touches on calculating the angle between scalar fields and introduces the unit tangent vector. The content is tailored to clarify concepts and solve related problems, making it an engaging resource for higher education students.
Takeaways
- 📚 The video introduces two main topics in Vector Calculus: 'Vector Differentiation' and 'Vector Integration'.
- 🧭 The importance of direction in vectors is emphasized, with 'i', 'j', and 'k' components representing the x, y, and z axes respectively.
- 🔍 The 'del' operator is introduced as a vector quantity used for vector differentiation, including its application on scalar and vector quantities.
- 📈 The concepts of 'gradient', 'divergence', and 'curl' are explained as outcomes of vector differentiation, with specific focus on their mathematical significance.
- 🔄 The 'gradient of f' is the differentiation of a scalar function, while 'divergence of f' and 'curl of f' are outcomes of differentiating vector functions.
- 🤔 The video clarifies when to use divergence (for scalar outputs) and curl (for vector outputs) in vector differentiation.
- 📐 The normal vector 'N' is explained as the gradient of a function, which is used to find the normal to a surface at a given point.
- 🔄 The concept of the unit normal vector is introduced, which involves finding the unit vector of the gradient.
- 📉 The video discusses 'directional derivative', explaining how to calculate it in a given direction using a specific formula.
- 🔗 The angle between two scalar fields is discussed, showing how to use the gradients of these fields to find the angle at a specific point.
- 🎯 Practical applications of the concepts are demonstrated through solving problems related to normal differentiation, velocity, acceleration, and unit tangent vectors.
Q & A
What are the two main topics discussed in the video?
-The two main topics discussed in the video are 'Vector differentiation' and 'vector integration'.
What is a vector quantity?
-A vector quantity is any quantity that denotes both magnitude and direction, typically represented with components along the x, y, and z axes denoted by 'i', 'j', and 'k'.
What is the differentiate operator in vector calculus?
-The differentiate operator in vector calculus is denoted by 'del', and it is used for differentiating vector functions.
What is the 'gradient of f' in the context of vector calculus?
-The 'gradient of f' is the result of applying the 'del' operator on a scalar quantity, and it represents the direction of the greatest rate of increase of the scalar function.
What are the two types of products between two vectors?
-The two types of products between two vectors are the dot product and the cross product.
How is the dot product of two vectors calculated?
-The dot product of two vectors is calculated by multiplying corresponding components and summing the results.
What is the determinant of a matrix used for in the context of vector calculus?
-In the context of vector calculus, the determinant of a matrix is used to calculate the cross product of two vectors.
What is the 'divergent of f' and what is its significance?
-The 'divergent of f' is the dot product of the 'del' operator and a vector function, and it represents the quantity of a vector field that is directed outward from a given point.
What is the 'curl of f' and when should it be used?
-The 'curl of f' is the cross product of the 'del' operator and a vector function, representing the rotation or circulation of a vector field. It should be used when finding the output of a vector differentiation into a vector form.
What is the normal vector and how is it found?
-The normal vector is a vector perpendicular to a surface, denoted by 'N', and it is found by calculating the gradient of a scalar function.
What is the unit normal vector and how is it calculated?
-The unit normal vector is a normal vector with a magnitude of one. It is calculated by finding the normal vector and then dividing it by its magnitude to normalize it.
What is a directional derivative and how is it found?
-A directional derivative is the rate at which a scalar function changes in a particular direction. It is found using the formula that involves the gradient of the scalar function and the unit vector in the direction of interest.
How can you find the angle between two scalar quantities using their gradients?
-To find the angle between two scalar quantities, you calculate the gradients of both functions at a given point and then use the dot product formula along with the magnitudes of the gradients to find the cosine of the angle between them.
What is the tangent vector and how is it related to the position vector?
-The tangent vector is a vector that is tangent to a curve or surface at a given point. It is related to the position vector by being a derivative of the position vector with respect to a parameter that describes the curve or surface.
What is the unit tangent vector and how is it found?
-The unit tangent vector is a tangent vector with a magnitude of one. It is found by taking the derivative of the position vector with respect to the parameter and then normalizing it.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
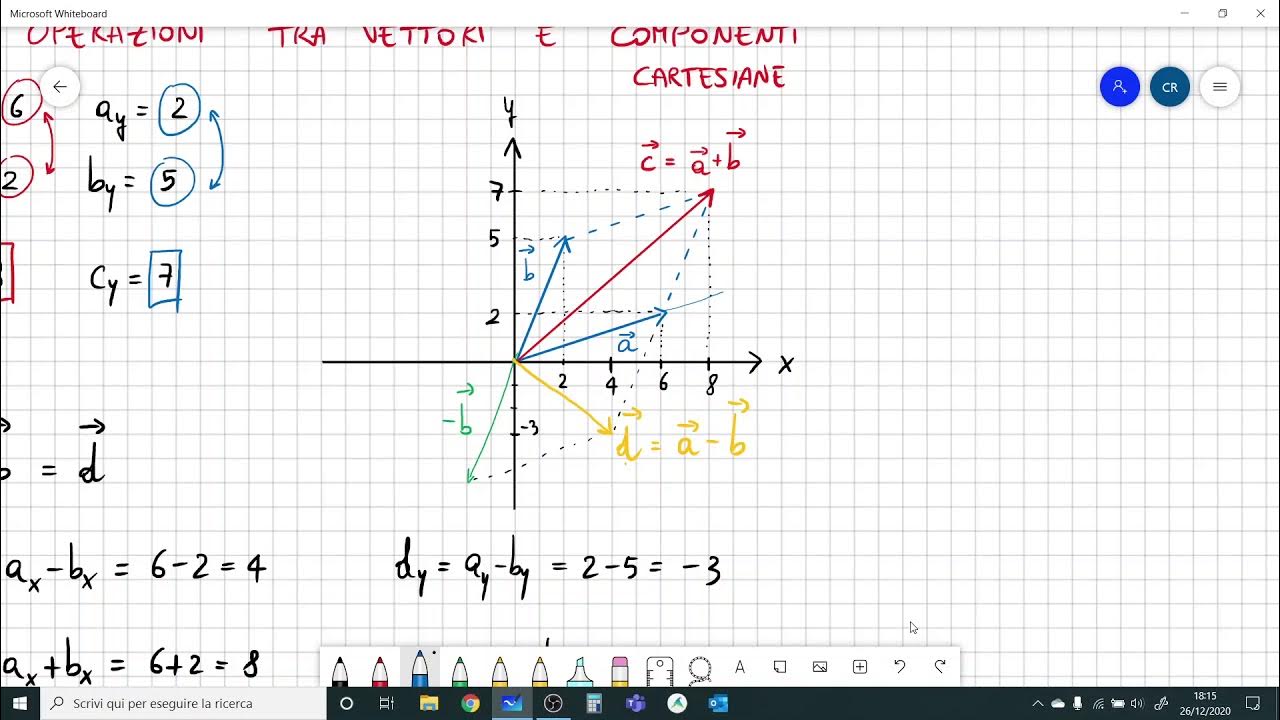
Operazioni tra vettori in componenti cartesiane
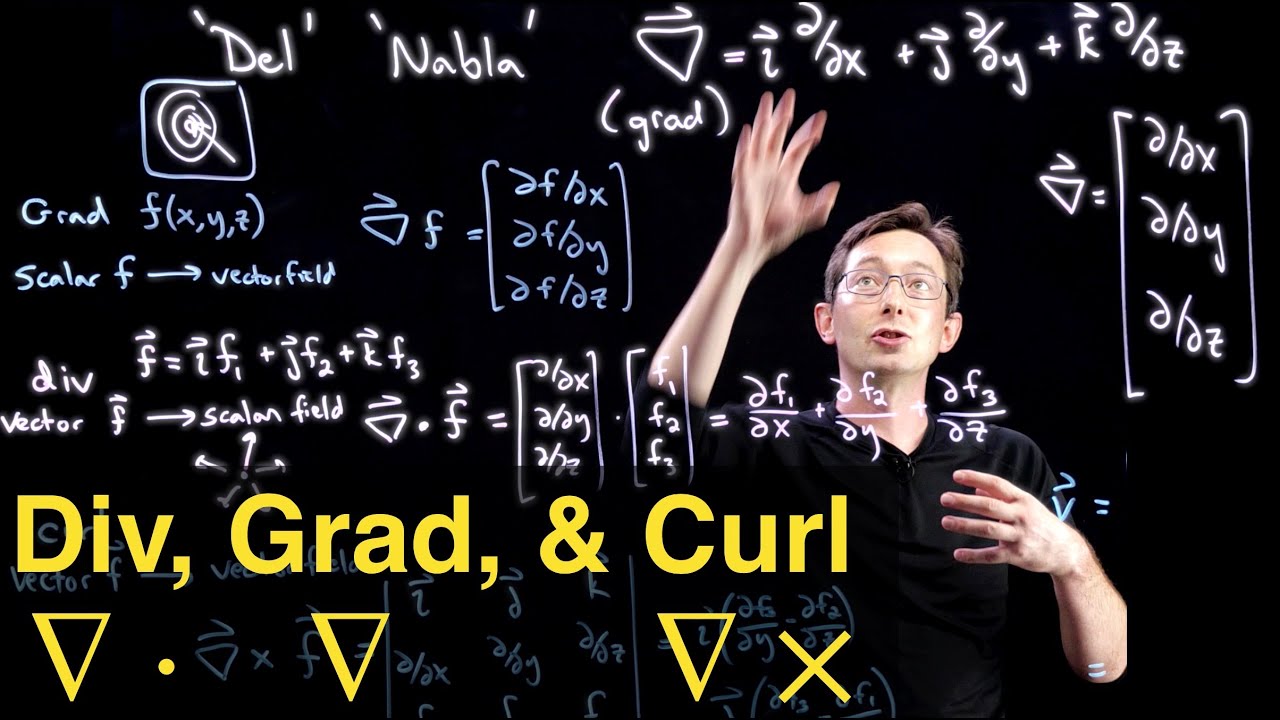
Div, Grad, and Curl: Vector Calculus Building Blocks for PDEs [Divergence, Gradient, and Curl]
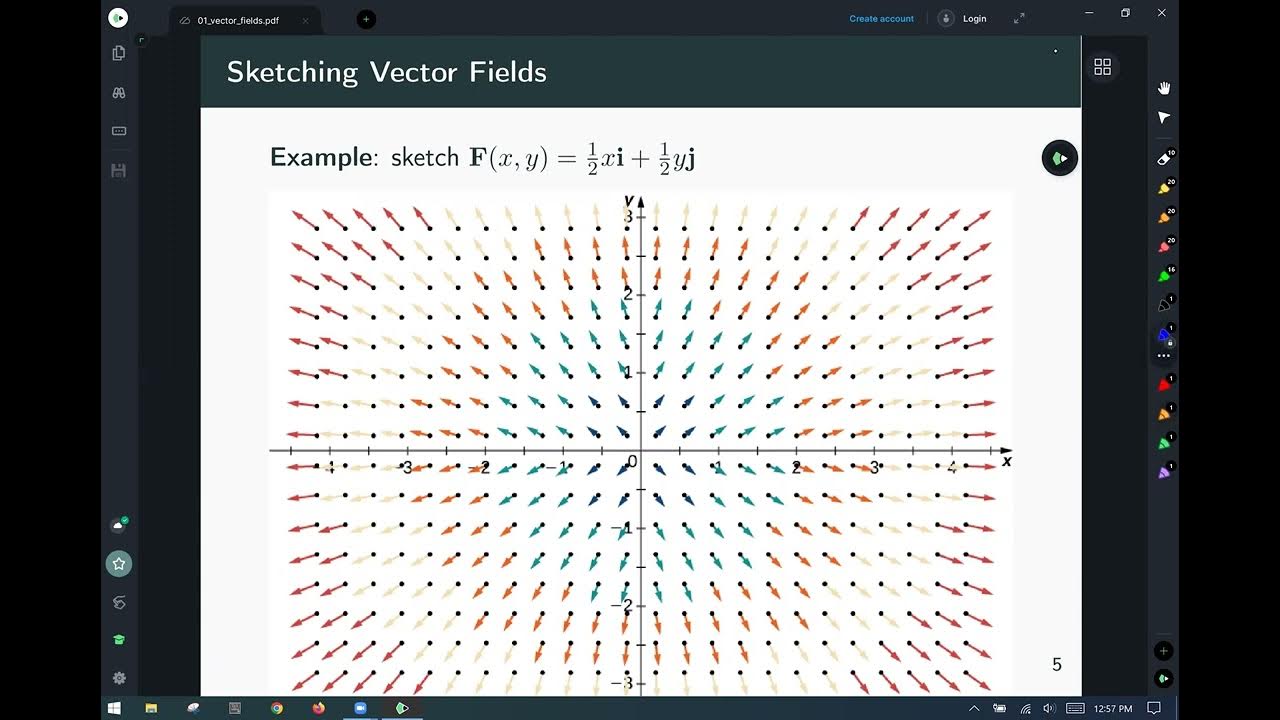
calc 3 vector fields

Formalisme dalam Mekanika Kuantum: Ruang vektor

Matematika Teknik II: 223 Kalkulus Vektor - Persamaan Parametrik Kurva dalam Ruang

Divergence and Curl of vector field | Irrotational & Solenoidal vector
5.0 / 5 (0 votes)