Kinematics Part 3: Projectile Motion
Summary
TLDRIn this educational video, Professor Dave explores projectile motion, a concept where objects move both horizontally and vertically. He explains that the motion can be broken down into independent horizontal and vertical components, each with its own equations. Using the example of a rock thrown at a 30-degree angle from a cliff, he demonstrates how to calculate time in the air and horizontal distance traveled. The video simplifies the complex idea of projectile motion by relating it to one-dimensional motion, encouraging viewers to understand the principles through real-world application.
Takeaways
- 📚 Projectile motion involves an object moving in both horizontal and vertical directions, typically thrown or launched into the air.
- 🔍 Kinematic equations can be used to describe projectile motion by separating it into horizontal (x-direction) and vertical (y-direction) components.
- 🏋️♂️ Horizontal and vertical motions in projectile motion are independent, meaning they can be analyzed separately.
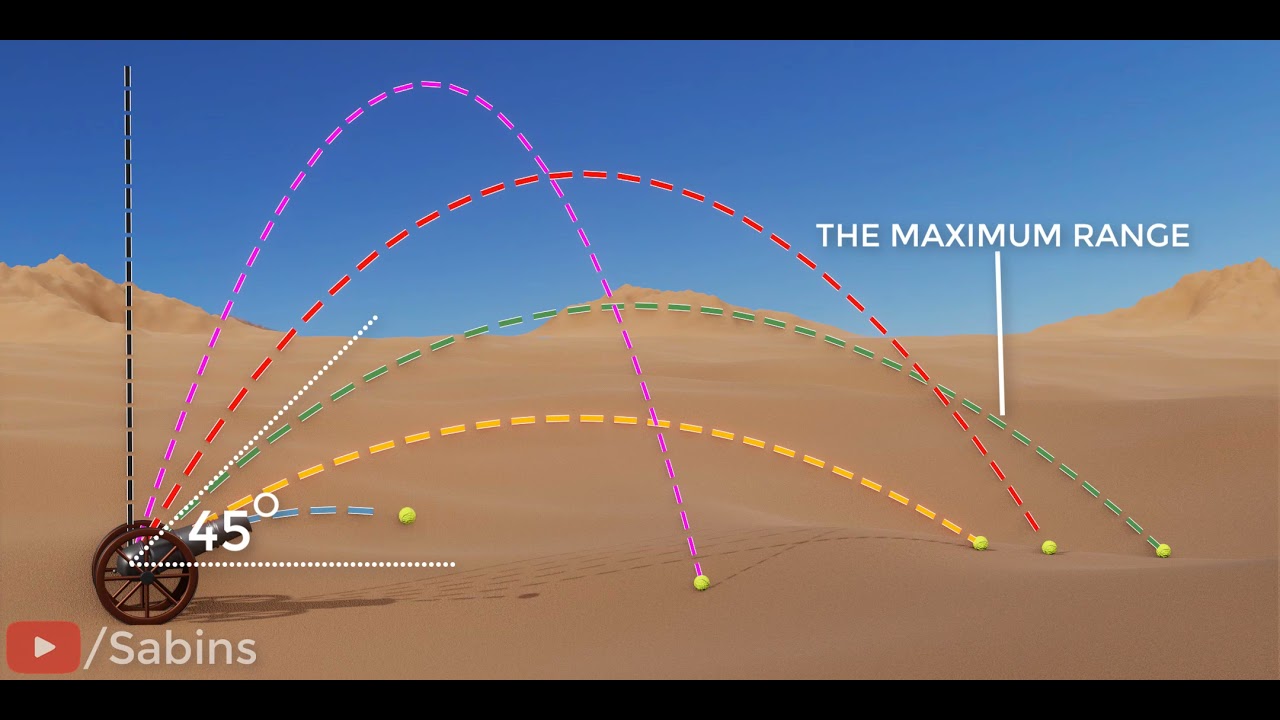
- 🎯 The path of a projectile is represented by a parabolic trajectory, influenced by the initial launch angle and velocity.
- 🕒 The time an object spends in the air during projectile motion is determined solely by its vertical motion.
- 📏 The horizontal distance traveled by a projectile is influenced by both its horizontal velocity and the time it is in the air.
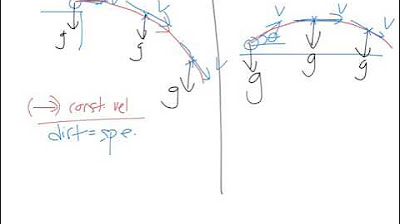
- 📐 To analyze projectile motion, the initial velocity vector is split into its horizontal (Vx) and vertical (Vy) components using trigonometric functions.
- 📉 The vertical velocity of a projectile decreases due to gravity until it reaches the peak (zenith) and then becomes increasingly negative as it falls.
- ⏱️ The time a projectile is in the air can be calculated using the vertical motion equations, treating it as a one-dimensional vertical motion problem.
- 📐 The horizontal distance a projectile travels can be calculated by multiplying the horizontal velocity by the time the object is in the air.
Q & A
What is projectile motion?
-Projectile motion is the motion of an object that is thrown or launched into the air, moving in both horizontal and vertical directions simultaneously. It can be represented by a parabolic path.
Why are the horizontal and vertical motions of a projectile considered independent?
-The horizontal and vertical motions of a projectile are considered independent because they can be described by separate equations, with horizontal motion unaffected by gravity and vertical motion influenced only by gravity.
How does the time it takes for a projectile to hit the ground relate to its motion?
-The time it takes for a projectile to hit the ground is determined solely by its vertical motion, as it will stop being in the air when it reaches the ground, regardless of its horizontal velocity.
What is the significance of the initial velocity's angle in projectile motion?
-The angle of the initial velocity determines the direction and the distribution of the motion into horizontal and vertical components, which in turn affects the range and maximum height of the projectile.
How can the initial velocity vector of a projectile be split into horizontal and vertical components?
-The initial velocity vector of a projectile can be split into horizontal (Vx) and vertical (Vy) components using trigonometric functions: Vx = V * cos(θ) and Vy = V * sin(θ), where V is the initial velocity and θ is the angle of projection.
What is the effect of gravity on the vertical velocity component of a projectile?
-Gravity causes a constant acceleration in the negative direction on the vertical component of a projectile's velocity, causing it to decrease until it reaches zero at the peak (zenith) and then become increasingly negative until it hits the ground.
How can you calculate the time a projectile spends in the air?
-The time a projectile spends in the air can be calculated using the vertical motion equation, considering only the vertical component of the initial velocity and the acceleration due to gravity.
What determines the horizontal distance a projectile travels?
-The horizontal distance a projectile travels is determined by its horizontal velocity component and the time it spends in the air, as the horizontal motion is not affected by gravity.
Why are trigonometric functions necessary when analyzing projectile motion?
-Trigonometric functions are necessary to break down the initial velocity into its horizontal and vertical components, which allows for separate analysis of the motion in each direction.
Can you provide a real-world example of how projectile motion is analyzed using the concepts from the script?
-In the script, an example is given where a rock is thrown at a 30-degree angle with an initial velocity of 8.5 m/s from the edge of a 100-meter cliff. The analysis involves calculating the time in the air and the horizontal distance traveled using the principles of projectile motion.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenant5.0 / 5 (0 votes)