Slope, Line and Angle Between Two Lines |Analytic Geometry|

Summary

This video tutorial offers a quick method for calculating the angle between two lines using the concept of slope. It explains the relationship between slope and angle of inclination, and how to determine if lines are parallel or perpendicular based on their slopes. The main formula for finding the angle between two intersecting lines is provided, along with an alternative strategy that involves understanding the tangent of the angle as the difference in slopes. The video also covers different forms of line equations, including point-slope and slope-intercept forms, to aid in the calculation process. The presenter concludes with an example to illustrate the application of these concepts.

Takeaways

• 📚 The video teaches how to find the angle between two lines using the fastest method.
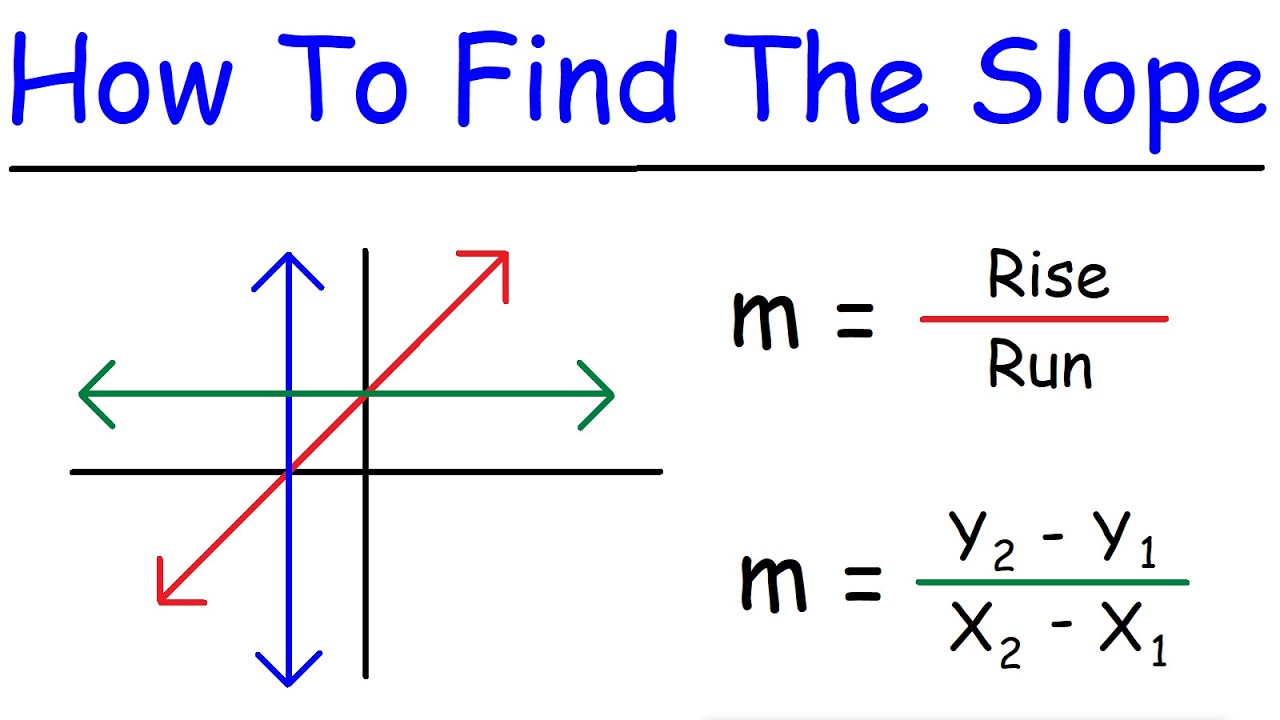
• 📐 The slope (m) of a line is calculated by the formula \( m = \frac{y_2 - y_1}{x_2 - x_1} \).
• 📈 The angle of inclination (θ) of a line is related to its slope through the tangent function, \( \tan(\theta) = m \).
• 🔄 If two lines are parallel, they have the same slope.
• ⊥ If two lines are perpendicular, one line's slope is the negative reciprocal of the other's.
• 🤔 The formula to find the angle between two intersecting lines with slopes m1 and m2 is \( \theta = \arctan\left(\frac{m2 - m1}{1 + m1 \cdot m2}\right) \).
• 💡 An alternate solution to finding the angle between two lines is by considering the difference between the angles of inclination of each line.
• 📝 The point-slope form of a line is \( y - y_1 = m(x - x_1) \).
• 📑 The slope-intercept form of a line is \( y = mx + b \), where m is the slope and b is the y-intercept.
• 📍 The two-point form of a line is derived from two points and is \( y - y_1 = \frac{y_2 - y_1}{x_2 - x_1}(x - x_1) \).
• 📉 The intercept form of a line is \( \frac{x}{a} + \frac{y}{b} = 1 \), where a and b are the x and y intercepts, respectively.
• 🔢 The video provides an example of finding the angle between two lines with given equations, emphasizing the use of the slope and the arctan function.

Q & A

What is the basic concept of slope in the context of this video?

The slope, denoted as 'm', is the ratio of the change in the y-coordinate (rise) to the change in the x-coordinate (run), mathematically represented as \( m = \frac{y_2 - y_1}{x_2 - x_1} \).

How is the angle of inclination of a line related to its slope?

The angle of inclination, denoted as 'theta', is related to the slope through the tangent function, where \( \tan(\theta) = m \), meaning the angle is the arctangent of the slope.

What does it mean if two lines have the same slope?

If two lines have the same slope, it means they are parallel to each other.

How can you determine if two lines are perpendicular based on their slopes?

Two lines are perpendicular if the product of their slopes \( m_1 \times m_2 \) equals -1, i.e., \( m_1 = -\frac{1}{m_2} \).

What is the formula for finding the angle between two intersecting lines given their slopes?

The formula to find the angle between two lines with slopes \( m_1 \) and \( m_2 \) is \( \theta = \arctan\left(\frac{m_2 - m_1}{1 + m_1m_2}\right) \).

What is an alternative method to find the angle between two lines without using the standard formula?

An alternative method involves finding the individual angles of inclination for each line (theta1 and theta2) and then calculating the difference, \( \theta = \theta_2 - \theta_1 \).

What is the point-slope form of a line equation and how is it used in this context?

The point-slope form is given by \( y - y_1 = m(x - x_1) \), where \( m \) is the slope and \( (x_1, y_1) \) is a point on the line. It's used to describe the line in terms of a point and its slope.

What is the slope-intercept form of a line equation and what does it represent?

The slope-intercept form is \( y = mx + b \), where \( m \) is the slope and \( b \) is the y-intercept. It represents the line's equation with respect to its slope and the point where it crosses the y-axis.

Can you explain the two-point form of a line equation and how it differs from the other forms?

The two-point form is derived from two points \( (x_1, y_1) \) and \( (x_2, y_2) \) on the line and is given by \( \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \). It differs from other forms as it does not explicitly require the slope to be known.

What is the intercept form of a line equation and how is it used?

The intercept form is \( \frac{x}{a} + \frac{y}{b} = 1 \), where \( a \) and \( b \) are the x and y intercepts, respectively. It's used when the intercepts are known to describe the line without needing the slope.

How does the video suggest finding the slope of a line given its equation in standard form?

The video suggests rearranging the standard form equation to the slope-intercept form, \( y = mx + b \), to easily identify the slope \( m \) as the coefficient of \( x \).

What is the final step in the video's method for finding the angle between two lines?

The final step is to use the arctangent function with the calculated values to find the angle in degrees, ensuring the calculator is in degree mode.