Trig Integrals Tan Sec
Summary
TLDRThis video script delves into the integration of trigonometric functions, specifically focusing on combinations of tangent and secant. It outlines methods for tackling integrals with these functions, including substitution strategies for cases where the exponents are both odd or even, and the use of trigonometric identities. The script provides step-by-step examples, such as integrating tangent cubed times secant cubed, and demonstrates the application of reduction formulas and integration by parts for more complex scenarios, offering a comprehensive guide to solving advanced trigonometric integrals.
Takeaways
- 📚 The video discusses integrals involving trigonometric functions, specifically combinations of tangent and secant.
- 🔍 The relationship between tangent squared and secant squared is highlighted, where secant squared is 1 + tangent squared and vice versa.
- 📐 The integral of tangent to the m power and secant to the n power dx is tackled in different cases based on the parity of m and n.
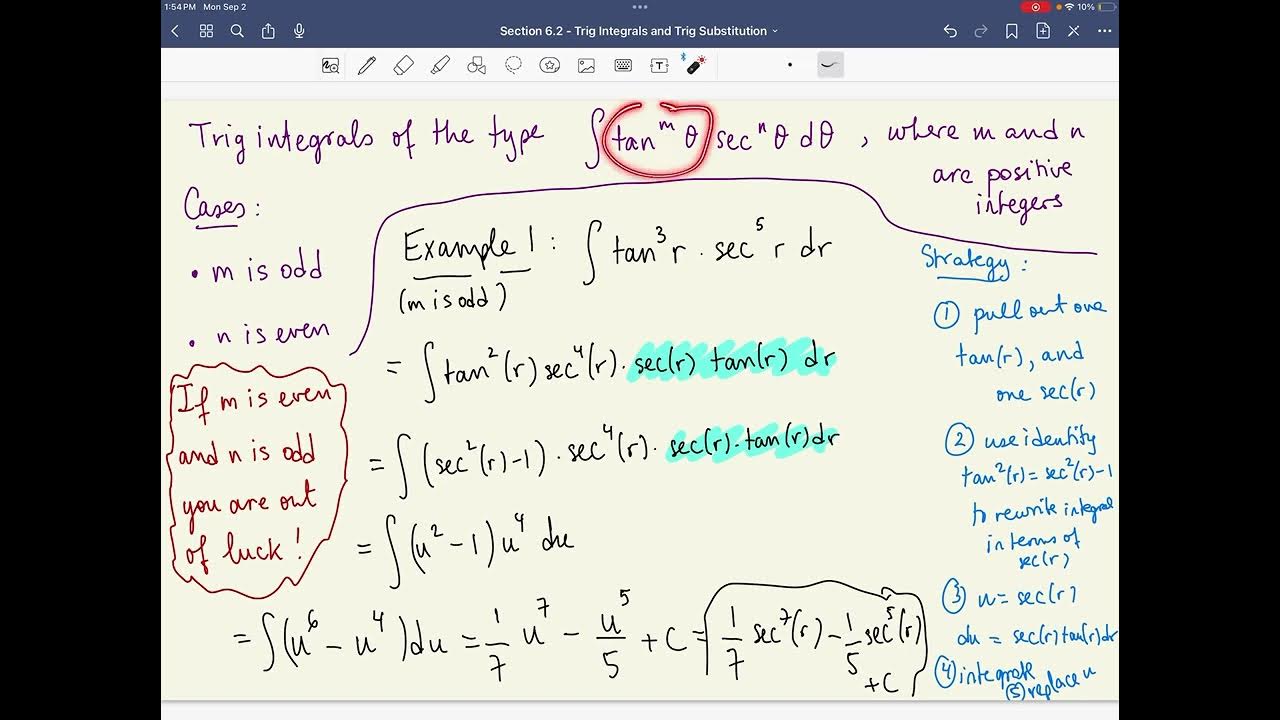
- 🎲 The first case involves both m and n being odd integers, exemplified by the integral of tangent cubed x secant cubed x dx.
- 📉 A u-substitution technique is introduced where u is chosen to simplify the integral, such as letting u be cant x.
- 🔑 The identity tangent squared equals secant squared minus 1 is used to transform the integral into a more manageable form.
- 📈 The integral is simplified using algebraic manipulation and u-substitution, leading to an antiderivative in terms of u, which is then replaced back with the original trigonometric functions.
- 📝 The second case with both m and n being even integers is presented, such as the integral of tangent squared x secant squared x dx, resulting in a simpler antiderivative.
- 🤔 A third case where one exponent is odd and the other is even is explored, requiring a different approach and sometimes integration by parts.
- 🧩 The process of integration by parts is mentioned for cases where direct substitution is not feasible, such as when the powers of secant or tangent do not match up easily.
- 📚 The use of reduction formulas is alluded to for integrating odd powers of secant, which involves a recursive process of integration by parts.
- 📘 The final result of the integrals is expressed in terms of the original trigonometric functions, with constants of integration added.
Q & A
What is the relationship between tangent squared and secant squared?
-Tangent squared (tan^2) is equal to secant squared minus one (sec^2 - 1), and secant squared is equal to one plus tangent squared (1 + tan^2).
How can you express the integral of tangent to the m power and secant to the n power in terms of u-substitution?
-You can let u be a function of x that simplifies the integral, for example, u = tan(x) or u = sec(x), and then find du in terms of dx to perform the u-substitution.
What is the integral of tangent cubed x secant cubed x dx?
-The integral is found by u-substitution, where u = sec(x), and then simplifying the expression to u^2 - 1, leading to the anti-derivative of u^4 - u^2, which is u^5/5 - u^3/3 + C, and replacing u back with sec(x).
How do you handle the integral when both exponents m and n are even?
-When both exponents are even, you can perform a u-substitution where u is a function that simplifies the integral, such as u = tan(x), and then integrate u^2 du, which results in u^3/3 + C.
What is the integral of tangent to the 3rd power x secant to the 4th power x dx?
-This integral is solved by recognizing that the even power of secant can be the u-substitution, resulting in an integral of u^3 * (1 + u^2) du, which simplifies to u^4/4 + u^6/6 + C after anti-derivatives.
What is the approach when one exponent is odd and the other is even?
-When one exponent is odd and the other is even, you may need to use integration by parts or apply reduction formulas, especially when dealing with odd powers of secant.
How do you integrate secant cubed x dx?
-Integration by parts is used, setting u = sec(x) and dv = sec^2(x)dx, which leads to a recursive integral that simplifies to sec(x)tan(x)/2 + (1/2)ln|sec(x) + tan(x)| + C after applying the reduction formula.
What is the significance of the identity tan^2(x) + 1 = sec^2(x) in trigonometric integrals?
-This identity allows you to convert between tangent squared and secant squared, which is useful for simplifying integrals involving these trigonometric functions.
Can you provide an example of an integral that requires using both u-substitution and the identity tan^2(x) = sec^2(x) - 1?
-An example is the integral of tangent cubed x secant squared x dx, where you first use u-substitution with u = sec(x) and then apply the identity to simplify the expression before integrating.
What is a reduction formula and how is it used in trigonometric integrals?
-A reduction formula is a method used to simplify the integration of trigonometric functions with higher powers by reducing the power through integration by parts or other techniques, making the integral more manageable.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahora5.0 / 5 (0 votes)