Fracciones parciales caso 2
Summary
TLDREl guión del video ofrece una explicación detallada sobre cómo expresar una fracción racional en fracciones parciales. Se analiza el denominador, se factoriza y se identifican las restricciones. Seguidamente, se descompone la fracción original en términos de fracciones parciales, utilizando técnicas como el uso de fórmulas notables y la distribución algebraica. El proceso culmina en el establecimiento de un sistema de ecuaciones para resolver los coeficientes A, B y C, obteniendo así la representación en fracciones parciales del polinomio dado.
Takeaways
- 📚 El ejercicio 119 trata sobre la expresión en fracciones parciales de una fracción racional dada.
- 🔍 Se analiza el denominador para determinar si está factorizado o si puede serlo, y se identifica que es un producto notable.
- 📐 Se factoriza el denominador como x(x - 1)^2 y se distribuye el numerador entre este denominador factorizado.
- 📝 Se establecen las restricciones para la fracción parcial, que son x = 0, x = 1 y x = -1.
- 📈 Se utiliza el método de fracciones parciales para descomponer la fracción en términos de x, (x - 1) y (x - 1)^2.
- 🧩 Se asignan letras a los factores para facilitar la resolución del sistema de ecuaciones resultante.
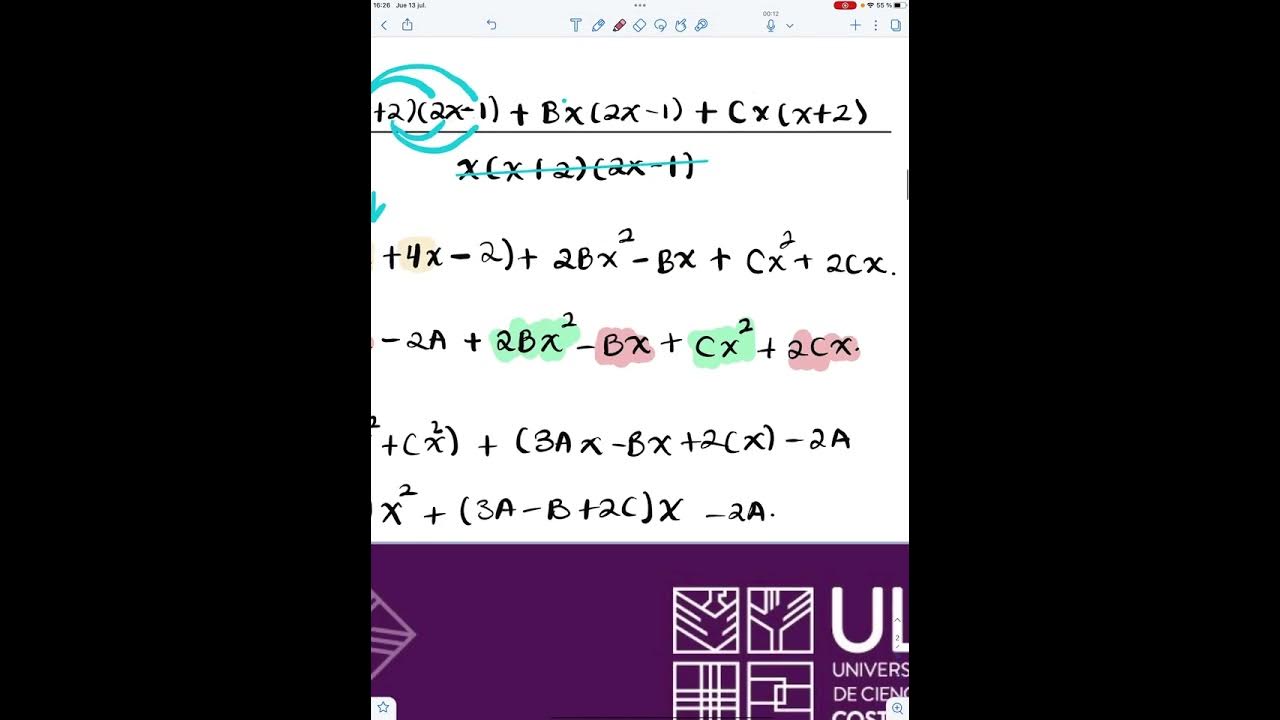
- 🔄 Se distribuyen los términos y se agrupan los coeficientes de x^2, x y los constantes.
- 📉 Se establece un sistema de ecuaciones para resolver los valores de A, B y C.
- 📌 Se resuelve el sistema de ecuaciones, encontrando los valores de A como 5, B como -3 y C como 6.
- 📝 Se reemplazan los valores de A, B y C en la fracción para obtener las fracciones parciales finales.
- 📑 El resultado final es la representación de la fracción racional en forma de fracciones parciales con los valores calculados.
Q & A
¿Qué es una fracción racional y cómo se expresa en fracciones parciales?
-Una fracción racional es una expresión matemática que combina un polinomio numerador y un polinomio denominador. Para expresar una fracción racional en fracciones parciales, se descompone en una suma de fracciones más simples, donde cada fracción tiene un factor del denominador como su denominador.
¿Cuál es el primer paso para expresar una fracción racional en fracciones parciales según el guión?
-El primer paso es estudiar el denominador y verificar si está factorizado. Si no lo está, se debe factorizar para poder proceder con la descomposición en fracciones parciales.
¿Cómo se factoriza el denominador dado en el guión?
-El denominador se factoriza sacando una x común y luego aplicando el producto notable, resultando en x(x - 1)^2.
¿Por qué es importante dejar el denominador expresado como un producto notable?
-Es importante para identificar claramente los factores que se repetirán en las fracciones parciales y para facilitar el proceso de descomposición.
¿Cómo se asignan las letras a las fracciones parciales en el caso de un denominador factorizado al cuadrado?
-Se asigna una letra a cada factor del denominador, y cuando un factor se repite, se asigna la misma letra con un exponente correspondiente a la cantidad de repeticiones, como en el caso de (x - 1)^2 donde se escribe B/(x - 1)^2.
¿Cuáles son las restricciones para la fracción dada en el guión?
-Las restricciones son los valores que hacen que el denominador sea cero, en este caso, x = 0, x = 1 y x = -1.
¿Cómo se resuelve el sistema de ecuaciones para encontrar los valores de A, B y C en las fracciones parciales?
-Se establecen las ecuaciones de igualdad entre los coeficientes de los términos de las fracciones parciales y los términos correspondientes del numerador original, y se resuelven para encontrar los valores de A, B y C.
¿Qué se hizo con el término independiente del numerador original, 5, en el proceso de descomposición en fracciones parciales?
-El término independiente 5 se asignó al término que no contiene x en la fracción parcial correspondiente a (x - 1)^2, lo que resultó en la ecuación C = 5.
¿Cómo se distribuyen los términos en el proceso de descomposición?
-Se distribuyen los términos multiplicando cada coeficiente A, B y C por los factores correspondientes del numerador, y se agrupan los términos con x al cuadrado, los términos con x y los términos independientes.
¿Cuál es la finalidad de la descomposición en fracciones parciales y cómo se aplica en el guión?
-La descomposición en fracciones parciales permite simplificar fracciones racionales y facilitar su integración o diferenciación. En el guión, se aplica para descomponer la fracción dada y encontrar sus fracciones parciales correspondientes.
¿Cómo se identifican los valores de A, B y C en las fracciones parciales resultantes?
-Se identifican al resolver el sistema de ecuaciones formado por igualar los coeficientes de los términos correspondientes en las fracciones parciales y el numerador original.
¿Qué valores se obtuvieron para A, B y C en el ejemplo del guión?
-Se obtuvieron los valores A = 5, B = -3 y C = 6 para las fracciones parciales.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahora5.0 / 5 (0 votes)