7. Kirchhoff Current Law ( KCL ) - Theory, Sign Conventions, Example Problem |BEE|
Summary
TLDRIn this educational video, the host explains the concept of Kirchhoff's Current Law (KCL), which states that the algebraic sum of currents at a junction is zero. They use a simple circuit diagram to demonstrate how to apply KCL to find unknown currents, emphasizing the importance of understanding incoming and outgoing current directions. The video also offers tips for solving more complex circuits, highlighting the need to identify junctions and form equations accordingly.
Takeaways
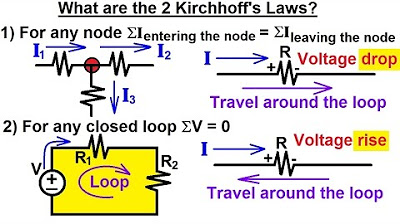
- 😀 The video discusses Kof's current law, also known as SKCL, which states that the algebraic sum of electric currents meeting at a junction is equal to zero.
- 🔌 A junction is defined as a point where three or more branches meet, and branches are parts of a circuit.
- 📈 Incoming currents at a junction are considered positive, while outgoing currents are considered negative.
- 🔄 The KCL can be referred to as the conservation of charge, emphasizing the balance of currents at a junction.
- 📚 The video provides an example to illustrate how to apply KCL in a circuit, involving currents labeled as i1, i2, i3, i4, and i5.
- 🔢 In the example, the KCL equation is formed by considering the sum of incoming currents (i1, i3, i4) equal to the sum of outgoing currents (i2, i5).
- 🔍 The video solves three sub-questions based on the circuit diagram, finding values for ix, iy, and iz under different conditions.
- 🤔 The video explains that in complex networks, you must identify all junctions, assume initial voltages, and form KCL equations for each junction.
- 🔋 The video mentions that in complex circuits, voltages and resistances will be involved, and Ohm's Law (V = IR) can be used to solve for currents and resistances.
- 📘 The video concludes by encouraging viewers to watch more videos on the channel for further understanding of complex circuits and the application of KCL.
Q & A
What is the main principle of Kirchhoff's Current Law (KCL)?
-Kirchhoff's Current Law states that the algebraic sum of the electric currents meeting at a junction or node is equal to zero. This means that the sum of incoming currents is equal to the sum of outgoing currents at any given node.
What is a junction in the context of electrical circuits?
-A junction is a point in an electrical circuit where three or more branches meet. It is the location where currents can either enter or leave the junction.
How are incoming and outgoing currents treated in KCL?
-In KCL, incoming currents are considered as positive, while outgoing currents are considered as negative. This helps in setting up the algebraic sum to zero for the currents meeting at a junction.
Can you explain the concept of conservation of charge in relation to KCL?
-The conservation of charge is a fundamental principle that states the total charge in an isolated system remains constant over time. In the context of KCL, this principle is reflected in the fact that the sum of currents at a junction must be zero, indicating that charge is neither created nor destroyed, just transferred between branches.
What is the significance of the direction of current in applying KCL?
-The direction of current is significant when applying KCL because it determines whether a current is considered incoming (positive) or outgoing (negative). If the direction is not given, it must be assumed for the purpose of setting up the KCL equations.
In the given example, how is the KCL equation set up for the circuit diagram?
-In the example, the KCL equation is set up by identifying the incoming and outgoing currents at the junction. The equation is formed by summing the incoming currents (5 amp, iZ, and iY) and setting it equal to the sum of the outgoing currents (IX and 3 amp).
What is the first condition given in the example for finding IX, and what is the result?
-The first condition given is when iY is equal to 5 amp and iZ is equal to 3 amp. Substituting these values into the KCL equation results in IX being equal to 10 amp.
How is the second condition in the example used to find the value of iY?
-The second condition states that IX is equal to 4 amp and iZ is equal to 4 times iY. By substituting these values into the KCL equation and solving for iY, it is found that iY equals 2 amp.
What does the third condition in the example tell us about the relationship between IX, iY, and iZ?
-The third condition states that IX is equal to iY, which is also equal to iZ. Using the KCL equation and substituting iZ for IX and iY, it is determined that iZ is equal to -2 amp, indicating that the current is flowing in the opposite direction.
What are some steps to follow when solving complex circuit problems using KCL?
-When solving complex circuits, one should first identify all junctions, assume initial voltages (VKN = 0), and unknown current directions. Then, form KCL equations for each junction. Remember sign conventions for adding or subtracting voltages, and use Ohm's Law (V = IR) to relate voltage, current, and resistance. These steps will help in solving for unknowns in more complicated circuits.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
5.0 / 5 (0 votes)