Challenging similarity problem | Similarity | Geometry | Khan Academy
Summary
TLDRThis script explores the use of similar triangles to determine the length of CF in a geometric diagram. By proving the similarity of triangles ABE and CFE, and DEB and CFB, and setting up equations based on the ratios of corresponding sides, the solution finds CF to be 36/7 units, highlighting a fascinating property of similar triangles.
Takeaways
- 📐 The problem involves determining the length of CF in a geometric diagram involving similar triangles.
- 🔍 Triangle CFE is similar to triangle ABE, which is inferred from their shared angles and embedded geometric structure.
- 🔍 Triangle CFB is also similar to triangle DEB, based on their corresponding angles and parallel lines.
- 📚 To prove similarity, the script demonstrates that corresponding angles in the triangles are congruent, fulfilling the angle-angle (AA) criterion for triangle similarity.
- 🔢 The script introduces variables: BE is assumed to be equal to y, and BF is denoted as x, with FE being y - x.
- 🔄 The ratios of corresponding sides in similar triangles are used to set up equations, leveraging the properties of similar triangles.
- 🧩 The script establishes that the ratio of CF to 9 (from triangle CFE) is equal to the ratio of y - x to y, and similarly, the ratio of CF to 12 (from triangle CFB) is equal to the ratio of x to y.
- 🔎 A key insight is that the ratio of CF to 9 can be rewritten as 1 - (CF/12), allowing for a substitution that simplifies the problem.
- ⚖️ The script solves for CF by combining the equations and finding a common denominator, ultimately leading to the equation 4CF + 3CF = 36.
- 📉 The final solution is CF = 36/7, demonstrating a universal height for the intersection point of strings draped from the tops of two objects to the base of the other, regardless of their distance apart.
- 🌐 The problem highlights a geometric principle where the height of the intersection point remains constant (36/7) for any given heights of 9 and 12, illustrating a fascinating property of similar triangles.
Q & A
What is the main problem discussed in the script?
-The main problem discussed in the script is to determine the length of CF in a geometric diagram involving similar triangles.
Why are triangles CFE and ABE considered similar?
-Triangles CFE and ABE are considered similar because they both have a 90-degree angle and share another angle, angle CEF, which is congruent to angle AEB.
How can you prove that triangles CFB and DEB are similar?
-Triangles CFB and DEB are similar because they both have a 90-degree angle and share another angle, angle DBE, which is congruent to angle CBF.
What is the significance of the angle shared by triangles CFE and ABE?
-The shared angle between triangles CFE and ABE is significant because it helps establish that the triangles are similar, which is a key step in solving the problem.
What assumption is made about the length of BE in the script?
-The script assumes that the length of BE is equal to y, which is a variable used to help solve the problem.
Why is it useful to assume that BE is equal to y?
-Assuming BE is equal to y is useful because BE is shared by both triangles ABE and DEB, and this assumption provides a starting point for setting up equations.
What variables are introduced for the lengths of BF and FE?
-The script introduces x as the variable for the length of BF and y - x for the length of FE.
How are the ratios of corresponding sides in similar triangles used in the script?
-The ratios of corresponding sides in similar triangles are used to set up equations that relate CF to the other sides of the triangles, ultimately helping to solve for CF.
What is the final equation derived to solve for CF?
-The final equation derived to solve for CF is CF/9 + CF/12 = 1, which simplifies to 7CF/36 = 1.
What is the final value of CF determined in the script?
-The final value of CF determined in the script is 36/7, or 5 and 1/7, regardless of the distance between the two triangles.
What insight does the problem provide about the intersection of strings draped from the tops of two objects?
-The problem shows that regardless of the distance between two objects, the point where the strings intersect will always be at a height of 36/7 from the base, illustrating a consistent geometric property.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Similar Triangles and Figures, Enlargement Ratios & Proportions Geometry Word Problems
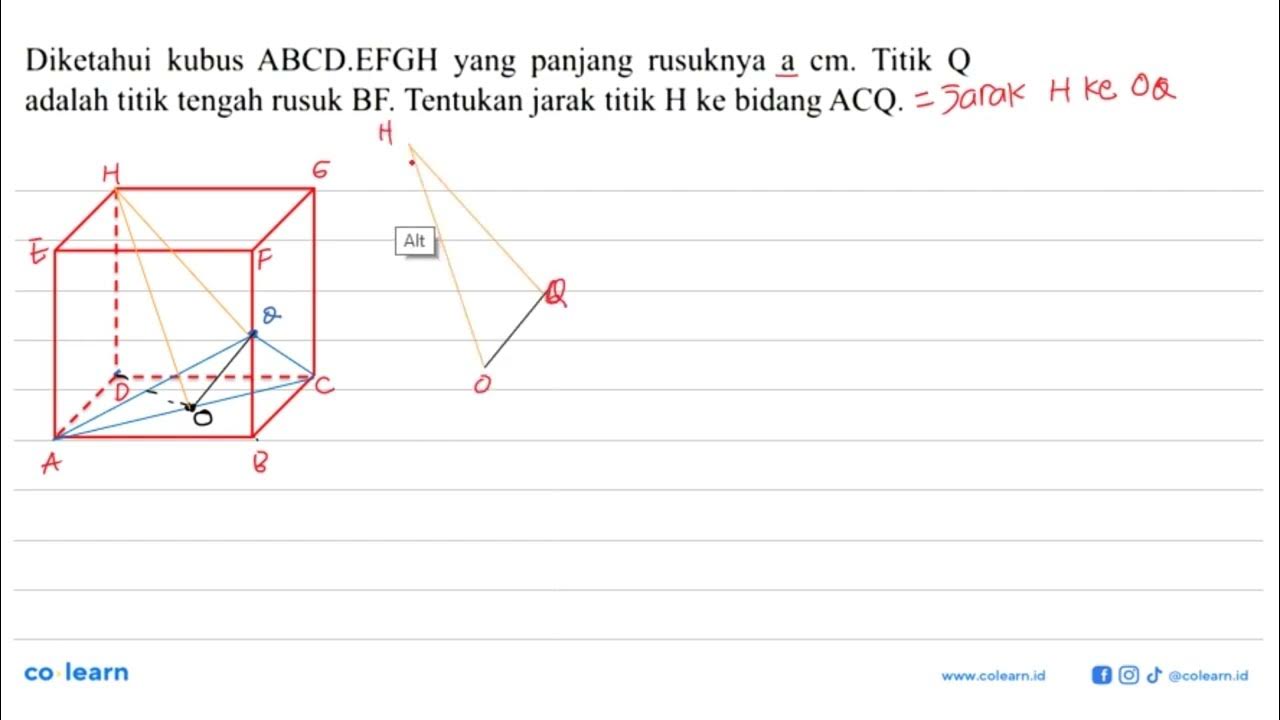
Diketahui kubus ABCD.EFGH yang panjang rusuknya a cm. Titik Q adalah titik tengah rusuk BF...
Similar Triangles - GCSE Maths

Appliquer le théorème de Thalès (1) - Troisième

KESEBANGUNAN DUA BANGUN DATAR

Kesebangunan Segitiga: Kesebangunan Segitiga Siku-siku (Belajar Matematika Kelas 7) - Kak Hasan
5.0 / 5 (0 votes)
