Drone Control and the Complementary Filter
Summary
TLDRThis video lecture introduces the concept of a complementary filter, a simple yet effective tool for blending data from different sensors, particularly useful in drone control systems. It explains how to estimate the roll angle using an IMU's gyro and accelerometer, highlighting the strengths and limitations of each method. The video demonstrates how integrating gyro data over time can accumulate errors, while accelerometer readings offer long-term stability despite short-term noise. It then illustrates the implementation of a complementary filter that combines the short-term accuracy of the gyro with the long-term stability of the accelerometer, providing a practical solution for more accurate roll angle estimation.
Takeaways
- 📚 The video introduces the concept of a complementary filter, a simple yet effective method for blending measurements from two different sensors.
- 🛠 The context of the explanation is a drone trying to estimate its roll angle using an IMU (Inertial Measurement Unit), which includes a gyroscope and an accelerometer.
- 🔄 The gyroscope measures angular rates and can be used to estimate the roll angle by integrating these rates over time, a method known as dead reckoning.
- 📉 Dead reckoning is susceptible to cumulative errors due to the integration of noise and bias in the gyroscope measurements, leading to inaccuracies over time.
- 🌐 The accelerometer measures acceleration, including gravity, and can be used to determine the roll angle by calculating the arctangent of the acceleration in the Y and Z directions.
- 🔍 While accelerometer measurements are stable long-term due to the constant gravity vector, they are noisy and can be affected by any acceleration, not just gravity.
- 🤝 The complementary filter combines the short-term accuracy of the gyroscope with the long-term stability of the accelerometer to produce a more reliable roll angle estimate.
- 🧩 The implementation of the filter involves using a low-pass filter on the accelerometer measurements and a high-pass filter on the gyroscope measurements, or a simplified approach by scaling and combining the two measurements.
- ⚙️ The filter can be tuned by adjusting the time constant for the low-pass filter, which affects the balance between short-term agility and long-term stability.
- 📉 The video demonstrates the effectiveness of the complementary filter through a JavaScript program, showing how it maintains a closer estimate to the true roll angle compared to using either sensor alone.
- 🔧 The video also discusses the discrete implementation of the filter in software, which involves scaling the gyroscope and accelerometer measurements and applying a low-pass filter to the sum.
Q & A
What is a complimentary filter in the context of control systems?
-A complimentary filter is a simple yet effective method used to blend measurements from two different sensors, such as an IMU's gyro and accelerometer, to estimate a variable like the roll angle of a drone more accurately than either sensor could alone.
Why is the roll angle estimation using only a gyroscope prone to error over time?
-Estimating the roll angle using only a gyroscope is prone to error over time because the integration of the angular rate measurements accumulates any bias or noise in the gyro readings, leading to a growing discrepancy between the estimated and true roll angles.
How does an accelerometer help in estimating the roll angle of a drone?
-An accelerometer measures the linear acceleration, including the acceleration due to gravity. By knowing the direction of gravity relative to the drone's reference frame, the roll angle can be determined, although this method is less precise in the short term due to noise and other accelerations.
What is the main advantage of using a complementary filter over relying solely on either the gyroscope or the accelerometer?
-The main advantage of using a complementary filter is that it combines the short-term accuracy of the gyroscope with the long-term stability of the accelerometer, resulting in a more reliable and accurate estimation of the roll angle.
How does the script describe the behavior of the gyroscope and accelerometer measurements over time?
-The script describes the gyroscope measurements as being smooth and less jittery in the short term due to integration, but slowly wandering over time. In contrast, the accelerometer measurements are more stable long term because the gravity vector doesn't change, but are noisy and less reliable in the short term.
What is the purpose of the low-pass filter in the context of the complementary filter?
-The purpose of the low-pass filter in the complementary filter is to attenuate high-frequency noise and emphasize the long-term stability provided by the accelerometer, while still allowing some of the short-term agility from the gyroscope measurements.
How is the high-pass filter related to the low-pass filter in the complementary filter?
-In the complementary filter, the high-pass filter is the complement of the low-pass filter, meaning that if the low-pass filter is represented by G(s), the high-pass filter is represented by 1 - G(s). When combined, they sum up to 1, ensuring the integrity of the original measurements.
What is the significance of the time constant 'tau' in the low-pass filter of the complementary filter?
-The time constant 'tau' in the low-pass filter determines the cutoff frequency of the filter. A lower 'tau' allows more high-frequency content from the gyroscope, while a higher 'tau' emphasizes more low-frequency content from the accelerometer.
Can you explain the discrete implementation of the complementary filter as described in the script?
-The discrete implementation of the complementary filter involves scaling the gyroscope and accelerometer measurements, summing them, and then applying a low-pass filter. This is done at each time step, updating the roll angle estimate by taking a fixed fraction of the gyroscope measurement and a complementary fraction of the accelerometer measurement.
How does the script demonstrate the effectiveness of the complementary filter through a JavaScript program?
-The script uses a JavaScript program to simulate the behavior of the complementary filter, showing how it holds close to the true down direction, unlike the gyroscope which wanders off, and the accelerometer which is noisy. The program visually demonstrates the filter's ability to balance short-term agility and long-term stability.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
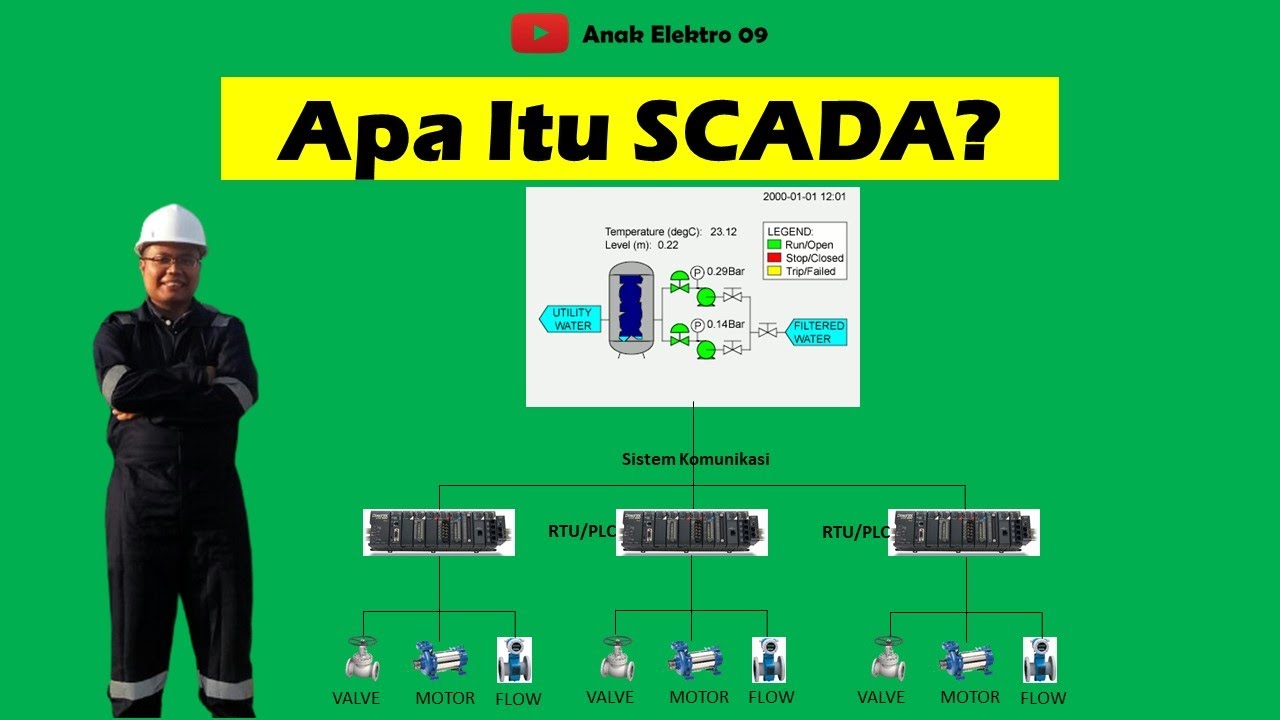
Pengenalan SCADA (Supervisory Control And Data Acquisition)
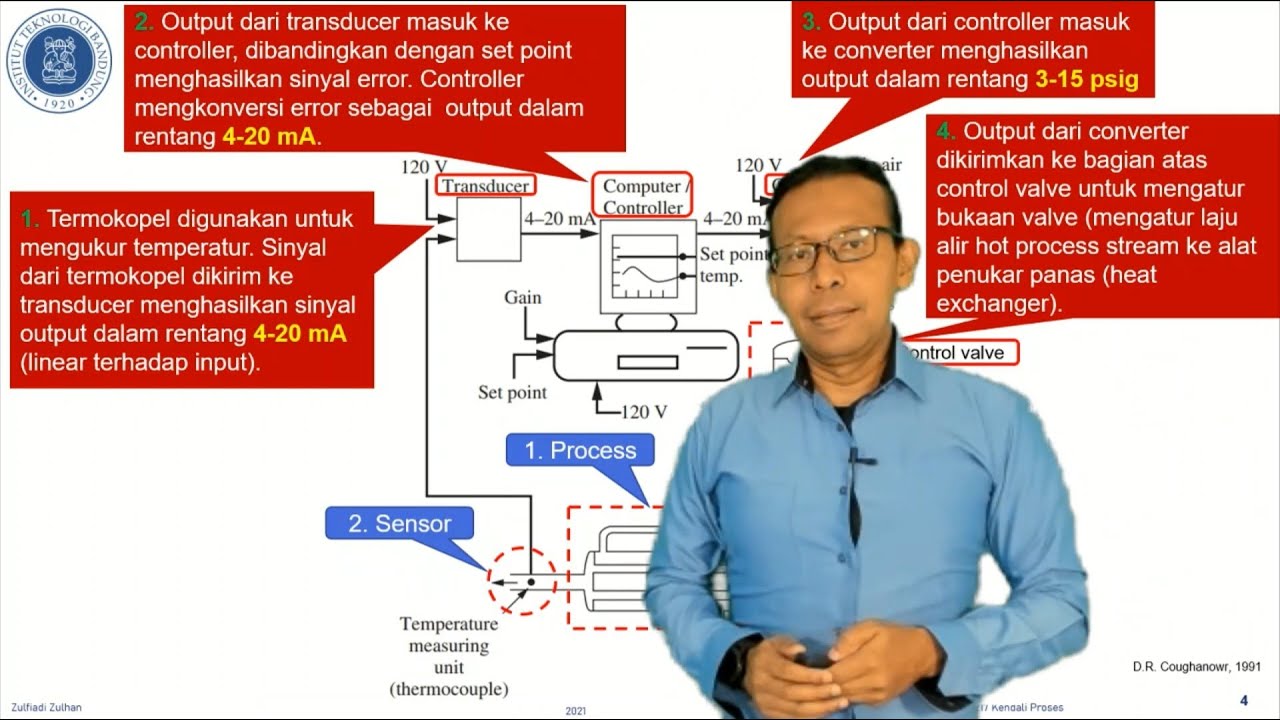
06. MG3217 Kendali Proses S01: Penyederhanaan Diagram Blok

Extended Kalman Filter - Sensor Fusion #3 - Phil's Lab #37

How a Quadcopter Works - Flight Mechanics, Components, & Sensors (2)

What Is PID Control? | Understanding PID Control, Part 1

Lec-2: Introduction to DBMS (Database Management System) With Real life examples | What is DBMS
5.0 / 5 (0 votes)
