Scalars and Vectors | Vector Addition | General Physics 1

Summary

This lesson on General Physics 1 introduces students to the concepts of scalars and vectors, covering the key differences between the two and how to perform vector addition. Scalar quantities, such as mass and time, only have magnitude, while vectors, like acceleration, include both magnitude and direction. The video demonstrates vector addition in one and two dimensions using examples, including the Pythagorean theorem and trigonometric functions to find resultant vectors. Key concepts like magnitude, direction, and using Cartesian planes for vector representation are explained, offering a clear guide for students to understand and apply vector addition.

Takeaways

• 😀 Scalars are physical quantities that only have magnitude, with no direction (e.g., mass, time, length).
• 😀 Vectors are physical quantities that have both magnitude and direction (e.g., velocity, acceleration).
• 😀 Scalar quantities can be represented as a simple line, while vectors are represented with an arrow showing direction.
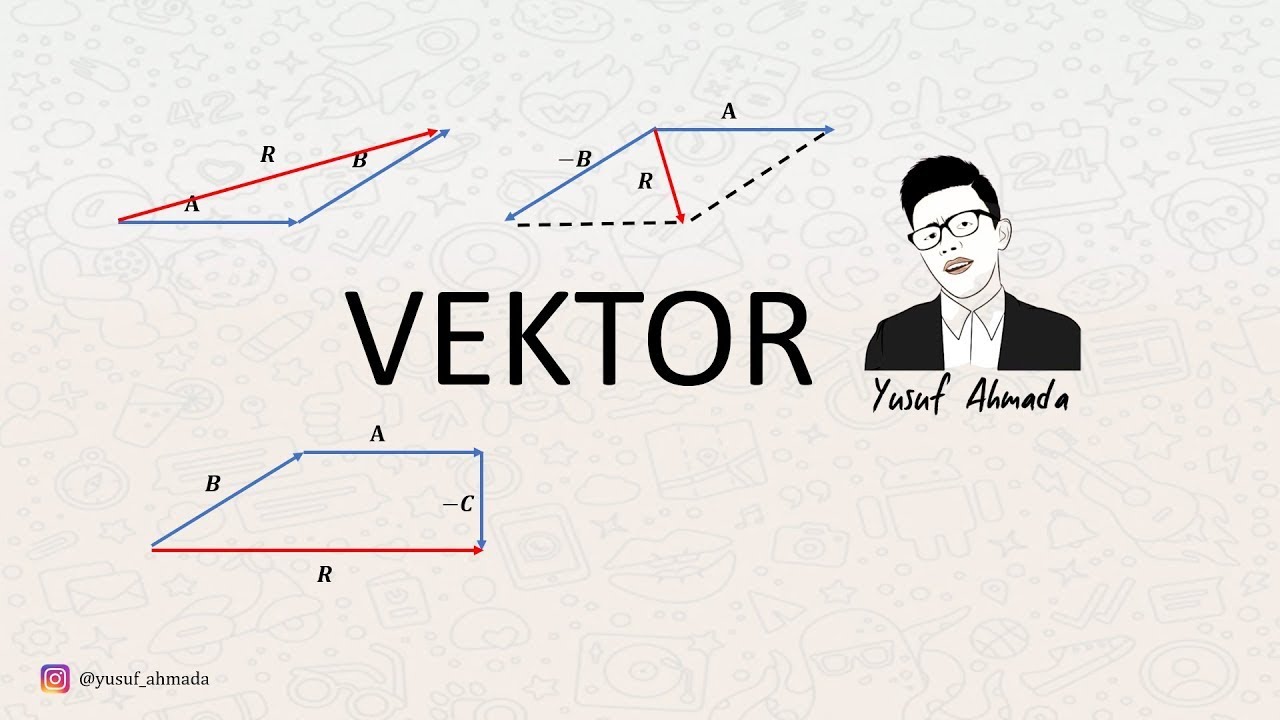
• 😀 Vector addition involves combining two or more vectors to form a resultant vector, which represents the combined magnitude and direction.
• 😀 When vectors are in the same direction, their magnitudes are simply added, and the direction remains the same.
• 😀 If vectors are in opposite directions, subtract the smaller vector’s magnitude from the larger one, and the resultant vector points in the direction of the larger vector.
• 😀 In two-dimensional vector addition, the vectors may form a right triangle, and the resultant vector can be calculated using the Pythagorean theorem.
• 😀 The direction of the resultant vector in two dimensions can be determined using the tangent formula to calculate the angle.
• 😀 The Pythagorean theorem can be used to calculate the magnitude of the resultant vector in two dimensions (c = √(a² + b²)).
• 😀 When using the arctangent to find the angle between two vectors, the angle is calculated as the ratio of the opposite side (B) to the adjacent side (A), then taking the arctangent of that value.

Q & A

What is the difference between scalars and vectors?

Scalars are physical quantities that only have magnitude, such as mass or time. Vectors, on the other hand, are physical quantities that have both magnitude and direction, like velocity or force.

What is a scalar quantity? Can you give an example?

A scalar quantity is a physical quantity that has only magnitude, with no associated direction. An example is mass, such as 500 grams, which is simply a size without any direction.

How is a vector represented visually?

A vector is represented by an arrow, with the tail indicating the starting point and the head indicating the direction. The length of the arrow shows the magnitude, and the direction of the arrow shows the direction of the vector.

What is the resultant vector?

The resultant vector is the sum of two or more vectors. It is a single vector that represents the combined effect of the original vectors.

How do you add two vectors in the same direction?

When two vectors are in the same direction, their magnitudes are added together. For example, if vector A is 6 km East and vector B is 2 km East, the resultant vector would be 8 km East.

How do you add two vectors that are in opposite directions?

When vectors are in opposite directions, the magnitude of the resultant vector is found by subtracting the smaller vector from the larger one. The direction of the resultant vector will be the same as the larger vector.

What happens when two vectors are in two different dimensions?

When two vectors are in two different dimensions, their addition forms a right triangle. The magnitude of the resultant vector can be calculated using the Pythagorean theorem, and the direction can be found using trigonometry.

How do you calculate the magnitude of a resultant vector in two dimensions?

To calculate the magnitude of a resultant vector in two dimensions, use the Pythagorean theorem: the square root of the sum of the squares of the magnitudes of the two vectors. For example, for vectors A (6 km East) and B (2 km North), the resultant vector magnitude is √(6² + 2²) = 6.32 km.

How do you find the angle of the resultant vector in two dimensions?

The angle of the resultant vector can be found using trigonometry. The tangent of the angle is the ratio of the opposite side (the smaller vector's magnitude) to the adjacent side (the larger vector's magnitude). Using arctangent, you can compute the angle.

What is the final direction of the resultant vector when vectors are 6 km East and 2 km North?

The direction of the resultant vector is found using the angle calculated with trigonometry. For vectors 6 km East and 2 km North, the direction is 18.2° North East, as the resultant vector lies between North and East on the Cartesian plane.