Nilai Mutlak • Part 1: Konsep, Definisi, Sifat, dan Fungsi Nilai Mutlak

Summary

In this video, the concept of absolute value is explained in depth, covering its definition as the non-negative distance of a number from zero on the number line. The script elaborates on essential properties, such as how the absolute value of a number is always positive or zero, and explores various operations involving absolute values. Additionally, the video introduces the absolute value function, explaining how it forms a V-shaped graph and its behavior across different types of functions. Practical examples and explanations are provided to solidify the viewer's understanding of this crucial mathematical concept.

Takeaways

• 😀 The absolute value of a number is its distance from zero on the number line, and it is always non-negative.
• 😀 Absolute value is denoted as |x|, and the absolute value of a number is the same regardless of its sign (positive or negative).
• 😀 For example, |2| = 2 and |-2| = 2, because both have the same distance from zero.
• 😀 If the number is greater than or equal to zero, the absolute value is equal to the number itself, e.g., |x| = x if x ≥ 0.
• 😀 If the number is less than zero, the absolute value is the negative of the number, e.g., |x| = -x if x < 0.
• 😀 The properties of absolute values include |x| = √(x²), which shows that the absolute value is the square root of the square of the number.
• 😀 Another property is that |x * y| = |x| * |y|, meaning the absolute value of the product is the product of the absolute values.
• 😀 The absolute value of a sum, |x + y|, is always less than or equal to |x| + |y|, a fundamental inequality known as the triangle inequality.
• 😀 Absolute values are useful in defining absolute value functions, which apply the concept of absolute value to various functions (e.g., linear, quadratic).
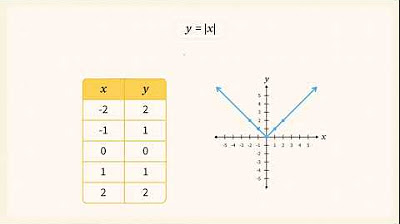
• 😀 In graphs, the absolute value function y = |x| forms a V-shape, with one line for positive x values (y = x) and one for negative x values (y = -x).

Q & A

What is the concept of absolute value in mathematics?

The absolute value of a number is the distance between that number and zero on the number line, without considering the direction. It is always a non-negative value.

How is the absolute value of a number represented?

The absolute value of a number 'x' is denoted as |x|, which is read as 'the absolute value of x'.

What is the absolute value of negative numbers?

The absolute value of a negative number is its positive counterpart. For example, |−2| = 2.

What happens to the absolute value of zero?

The absolute value of zero is simply 0, because the distance from zero to zero is zero itself.

How do you calculate operations involving absolute values?

In operations involving absolute values, you first calculate the absolute value of each number, then perform the other operations like addition, subtraction, multiplication, or division as usual.

What is the result of the absolute value operation |−6| × |1/3| + |4/3|?

The result is 8. First, calculate the absolute values: |−6| = 6, |1/3| = 1/3, and |4/3| = 4/3. Then, follow the multiplication and addition operations to get the final result.

How do you calculate the value of a function involving absolute value?

To calculate a function involving absolute value, substitute the value of 'x' into the function, compute the absolute value where needed, and then proceed with the rest of the operations.

What are some key properties of absolute values?

Some key properties of absolute values include: 1) |x| = |−x|, 2) |x| = √(x²), 3) |x| × |y| = |x × y|, 4) |x + y| ≤ |x| + |y|, and 5) |x − y| ≥ |x| − |y|.

How do absolute values affect the graph of a function?

The graph of a function involving absolute values typically forms a 'V' shape, with two linear segments. For example, the graph of y = |x| consists of two straight lines, y = x for x ≥ 0 and y = −x for x < 0.

What is the basic principle of the absolute value function?

The basic principle of the absolute value function is that it returns the input value if it's positive or zero, and the negation of the input value if it's negative. For example, f(x) = |x| returns x when x ≥ 0 and −x when x < 0.