How To Solve Absolute Value Equations, Basic Introduction, Algebra
Summary
TLDRThis video explains the concept of absolute value and how to solve equations involving it. The absolute value of a number is always positive or zero. Examples are provided, showing how to find solutions for equations like |x + 2| = 9, where x can be 7 or -11, and |2x - 5| = 1, where x can be 3 or 2. It also clarifies that absolute values cannot equal a negative number. The video walks through multiple examples step by step, making it easy to understand how to work with absolute value equations.
Takeaways
- 😀 The absolute value of a number is always positive, or zero if the number is zero.
- 👍 The absolute value of 5 is 5, and the absolute value of -8 is 8.
- 📈 An absolute value equation like |x| = 7 has two solutions: x = 7 or x = -7.
- 🔄 To solve absolute value equations, create two equations: one positive and one negative.
- 🔢 For |x + 2| = 9, the solutions are x = 7 and x = -11.
- ➕ For the equation |2x - 5| = 1, solving it results in two solutions: x = 3 and x = 2.
- ❌ If the absolute value function equals a negative number, such as |5x - 1| = -2, there is no solution.
- ✏️ When solving absolute value problems, isolate the absolute value expression before creating two equations.
- ➗ When solving |x - 1| = 3, the solutions are x = 4 and x = -2.
- 📝 The general approach to solving absolute value equations involves isolating the absolute value, setting up two equations, and solving them.
Q & A
What is the absolute value of a number?
-The absolute value of a number is its distance from zero on the number line, regardless of direction. It always produces a positive result, or zero if the number is zero.
What is the absolute value of 5?
-The absolute value of 5 is 5.
What is the absolute value of -8?
-The absolute value of -8 is 8.
Why can the absolute value never produce a negative result?
-The absolute value represents the distance from zero, which is always positive or zero. Therefore, it cannot produce a negative result.
What are the possible values of x if the absolute value of x equals 7?
-If the absolute value of x equals 7, x can either be 7 or -7, because both values satisfy the equation.
How do you solve an equation with absolute values, such as |x + 2| = 9?
-To solve |x + 2| = 9, write two equations: x + 2 = 9 and x + 2 = -9. Solving both gives x = 7 and x = -11.
What is the solution to the equation 2x - 5 = 1 and 2x - 5 = -1?
-For 2x - 5 = 1, adding 5 gives 2x = 6, then dividing by 2 gives x = 3. For 2x - 5 = -1, adding 5 gives 2x = 4, then dividing by 2 gives x = 2.
Why does the equation |5x - 1| = -2 have no solution?
-The equation |5x - 1| = -2 has no solution because the absolute value cannot equal a negative number.
How do you isolate the absolute value expression in an equation like |x - 1| = 7?
-To isolate the absolute value expression, first ensure the absolute value symbol is by itself on one side of the equation. For example, add or divide any constants before writing the two equations.
What are the possible values of x in the equation |x - 1| = 3?
-To solve |x - 1| = 3, write two equations: x - 1 = 3 and x - 1 = -3. Solving both gives x = 4 and x = -2.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Discrete Mathematics Lecture 8 | Domain & Range Of Function | One-One and Onto Function By GP Sir

NILAI MUTLAK PART I

Nilai Mutlak • Part 1: Konsep, Definisi, Sifat, dan Fungsi Nilai Mutlak

SOLVING QUADRATIC EQUATIONS BY EXTRACTING SQUARE ROOTS || GRADE 9 MATHEMATICS Q1
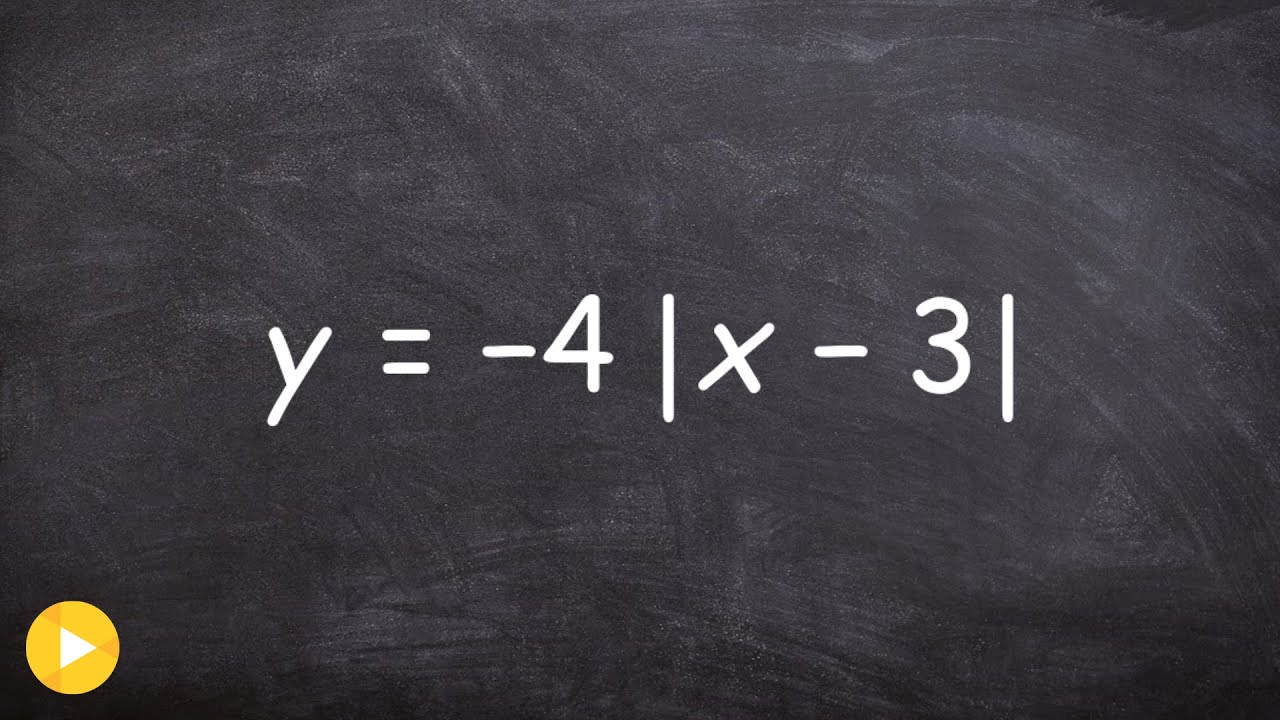
Learn how to graph an absolute value equation by identifying the vertex first

Matriks Matematika Kelas 11 • Part 23: Menyelesaikan SPLTV dengan Metode Determinan Matriks
5.0 / 5 (0 votes)