Probability Exponential Distribution Problems

Summary

This video explains how to solve probability problems involving exponential distributions. It walks through an example where the lifespan of laptops produced by Company XYZ follows an exponential distribution with a mean of 5 years. The video covers key concepts like calculating the rate parameter, writing the probability density function (PDF), and finding probabilities such as the chance a laptop lasts less than 3 years, more than 10 years, or between 4 and 7 years. The process involves using exponential distribution formulas and calculating areas under the curve for various probabilities.

Takeaways

• 😀 The lifespan of laptops produced by company XYZ follows an exponential distribution with a mean of 5 years.
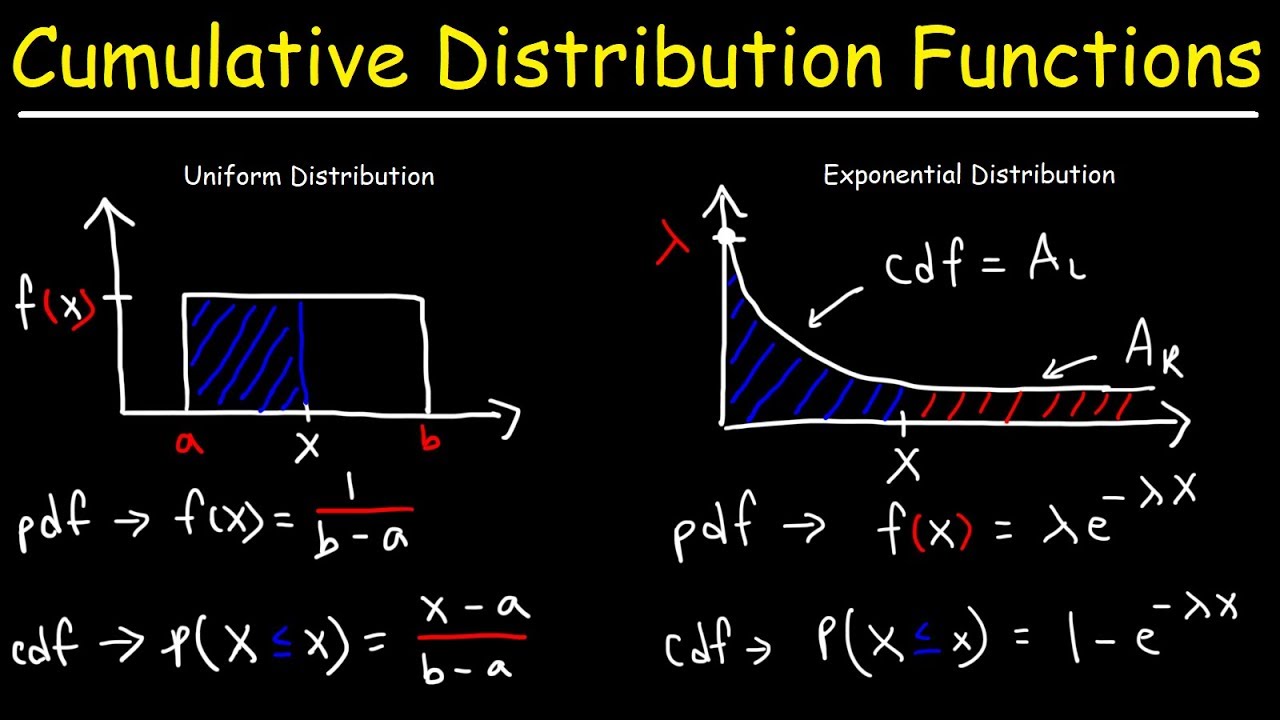
• 😀 The rate parameter (λ) of the exponential distribution is the reciprocal of the mean, calculated as 0.20 years⁻¹.
• 😀 The probability density function (PDF) for this exponential distribution is f(x) = 0.20 * e^(-0.20x).
• 😀 The y-intercept of the graph of the PDF represents the rate parameter, which is 0.20.
• 😀 To find the probability that a laptop lasts less than 3 years, we calculate the area under the curve from 0 to 3, yielding a 45.12% chance.
• 😀 The probability that a laptop lasts more than 10 years is found by calculating the area to the right of 10, which gives a 13.53% chance.
• 😀 The probability of a laptop lasting between 4 and 7 years is the difference between the probability of lasting less than 7 years and less than 4 years, resulting in a 20.27% chance.
• 😀 The formula to calculate the probability of an exponential distribution for a given value of X is P(X < x) = 1 - e^(-λx).
• 😀 When calculating probabilities, the value of the rate parameter (λ) directly affects the outcome, influencing the likelihood of the laptop lasting for a certain period.
• 😀 The exponential distribution is commonly used to model the lifespan of products and provides a straightforward way to calculate various probabilities based on the mean lifespan.

Q & A

What is the rate parameter in exponential distribution?

The rate parameter, represented by lambda (λ), is the reciprocal of the average lifespan. In the given problem, the average lifespan is 5 years, so λ = 1/5 = 0.20 (years^-1).

How is the probability density function (PDF) of an exponential distribution formulated?

The probability density function for an exponential distribution is given by f(x) = λ * e^(-λx), where λ is the rate parameter and x is the time variable.

What is the y-intercept of the exponential distribution graph?

The y-intercept of the graph of the exponential distribution corresponds to the rate parameter, which is 0.20 in this case. This is because when x = 0, e^0 = 1, so f(0) = λ * 1 = 0.20.

How do we calculate the probability that a laptop will last less than 3 years?

To calculate this probability, we use the formula P(X < 3) = 1 - e^(-λ * 3), where λ = 0.20. Substituting the values gives a result of approximately 0.4512, or a 45.12% chance.

What is the probability that a laptop will last more than 10 years?

The probability that a laptop lasts more than 10 years is given by P(X > 10) = e^(-λ * 10). Substituting λ = 0.20 gives e^(-2) ≈ 0.1353, or a 13.53% chance.

How do you calculate the probability that a laptop lasts between 4 and 7 years?

To calculate the probability that the laptop lasts between 4 and 7 years, we find P(4 < X < 7) = P(X < 7) - P(X < 4). Using the formula for the exponential distribution, we calculate each probability and subtract them, yielding approximately 0.2027, or a 20.27% chance.

What is the role of the exponential distribution in modeling the lifespan of laptops?

The exponential distribution is used to model the time between events in a Poisson process, such as the lifespan of a laptop. It helps quantify the probability of a laptop lasting a certain amount of time before failing.

What is the general formula used to calculate probabilities in exponential distributions?

The general formula for calculating probabilities in an exponential distribution is P(X < x) = 1 - e^(-λ * x) for probabilities less than a certain value, and P(X > x) = e^(-λ * x) for probabilities greater than a certain value.

How do you graph the exponential distribution?

To graph the exponential distribution, you plot the function f(x) = λ * e^(-λx) for different values of x. The graph starts at λ (the y-intercept) and decreases rapidly as x increases.

Why does the probability of a laptop lasting more than 10 years decrease exponentially?

The probability decreases exponentially because, as time passes, the likelihood of the laptop lasting longer decreases. The exponential distribution models this decreasing probability over time, with the rate of decay determined by the value of λ.