Peluang Kejadian Saling Lepas

Summary

This video script discusses the concept of probability, specifically focusing on the union of two events and how to calculate the probability of such events. It explores examples like the outcomes of rolling two dice and drawing cards from a deck. Key concepts covered include how to calculate the probability of events occurring together, dealing with overlapping events, and applying mathematical formulas to solve problems. The video also highlights various scenarios involving dice rolls and card draws, providing step-by-step calculations to illustrate the application of probability theory.

Takeaways

• 😀 The union of two events can be calculated using the formula: P(A or B) = P(A) + P(B) - P(A and B). This formula is crucial when events are not mutually exclusive.
• 😀 If two events are mutually exclusive (cannot happen together), the formula simplifies to: P(A or B) = P(A) + P(B).
• 😀 A common example involves throwing two dice. For instance, the probability of the sum of the dice being 5 or the difference being 1 is calculated using the union of events.
• 😀 In problems involving the union of events, it is important to subtract the intersection (where both events occur simultaneously) to avoid double-counting.
• 😀 When dealing with dice, if an event requires both a specific sum and a specific difference (e.g., sum of 6 and difference of 1), check if the intersection is possible. If not, the events are mutually exclusive.
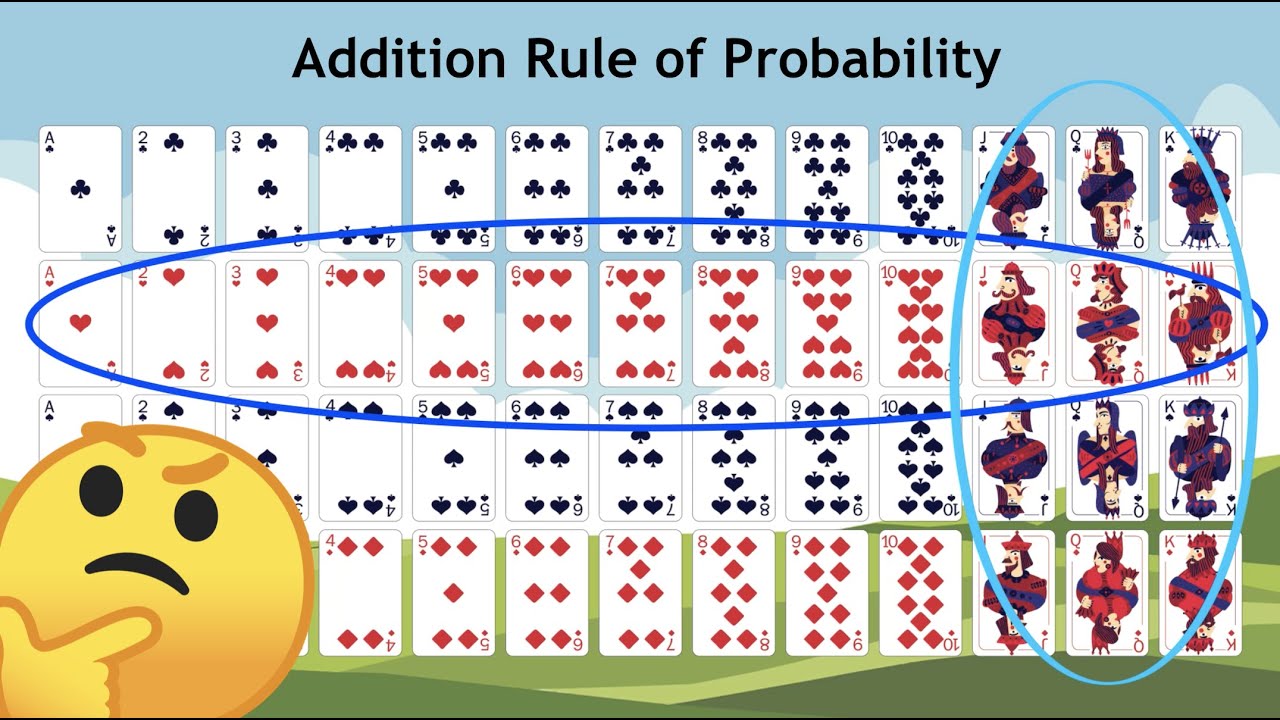
• 😀 The probability of drawing specific cards from a deck, such as even-numbered cards or prime-numbered cards, can also be calculated using the union of events formula.
• 😀 Events can be mutually exclusive, meaning there is no overlap between them, or they can have overlap, meaning they can both occur simultaneously.
• 😀 If there is no overlap between events, such as drawing a card that is both even and prime, the events are considered mutually exclusive.
• 😀 In some cases, calculating the probability of two events can involve evaluating all possible outcomes, such as the 36 possible outcomes when rolling two dice.
• 😀 The process of calculating the probability of compound events (like rolling a 5 or having a difference of 1) helps to understand the concept of event unions and intersections.

Q & A

What is the general concept being discussed in the script?

The script primarily discusses probability theory, focusing on the union and intersection of sets, as well as the concept of independent and dependent events in probability.

What does the union of two sets represent in probability?

The union of two sets in probability represents the event that either one or both events occur. It is denoted as P(A ∪ B), where A and B are the events.

How does the script explain the calculation of the probability of the union of two events?

The probability of the union of two events A and B is calculated using the formula P(A ∪ B) = P(A) + P(B) - P(A ∩ B), where P(A ∩ B) accounts for the overlap of events that have been counted twice.

What does the script say about 'disjoint events' or 'mutually exclusive events'?

Disjoint or mutually exclusive events are those that cannot occur at the same time. The script mentions that when events are disjoint, the probability of their union is simply the sum of their individual probabilities.

What is the example provided involving dice rolls?

The script includes an example of rolling two dice and calculating the probability of the sum of the dice being 5 or the difference being 1. The probability is calculated using the union of these two events.

How do you calculate the probability of two events with no intersection?

If two events have no intersection (i.e., they are disjoint), the probability of their union is the sum of their individual probabilities. For example, if the events A and B have no overlap, P(A ∪ B) = P(A) + P(B).

What is the significance of 'independent events' in probability?

Independent events are those where the occurrence of one event does not affect the occurrence of the other. In the script, this concept is indirectly referenced when discussing the calculation of probabilities for non-overlapping events.

How does the script explain the 'overlap' of two events in probability?

The overlap, or intersection, of two events is when both events occur simultaneously. The probability of this intersection must be subtracted when calculating the probability of their union to avoid double counting the overlapping cases.

What example involving a deck of cards is given in the script?

An example is given where a card is drawn from a deck, and the probability of drawing either an Ace or a red card is calculated. The script discusses how to compute the probability using the union of two events, while considering any overlap (Ace of red cards).

What is the formula for the probability of the union of two events?

The formula for the probability of the union of two events A and B is: P(A ∪ B) = P(A) + P(B) - P(A ∩ B). This accounts for the overlap of the two events, ensuring it is not double-counted.