Universo Mecánico 07 Integración

Summary

This video explores the historical journey leading to the discovery of integral calculus and its connection to differential calculus. It highlights the groundbreaking contributions of figures like Isaac Newton and Gottfried Wilhelm Leibniz, as well as earlier influences from Galileo, Kepler, and Archimedes. The script delves into the development of mathematical methods such as the method of exhaustion and the concept of limits, leading up to the formulation of calculus. It also examines the rivalry between Newton and Leibniz, the eventual recognition of their discoveries, and how their work has become a fundamental tool in science today.

Takeaways

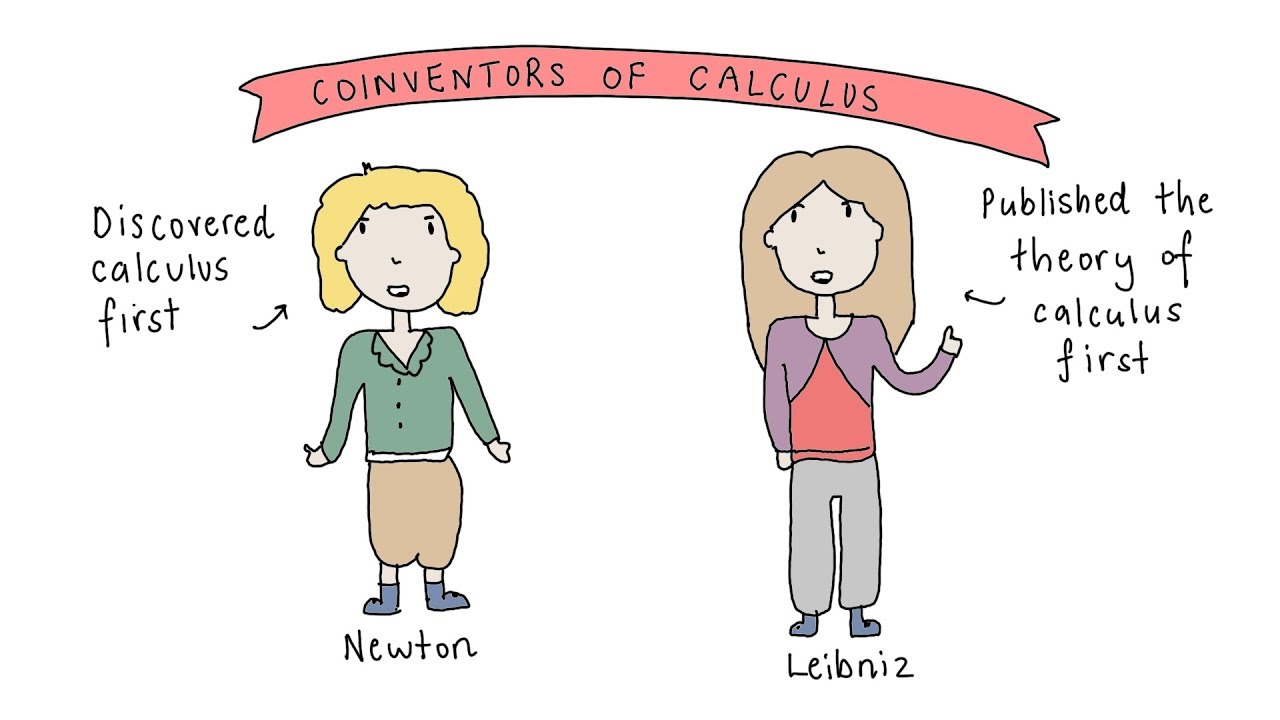
• 😀 Isaac Newton and Gottfried Wilhelm Leibniz are jointly credited with the discovery of calculus, though their methods and contributions differed.
• 😀 The discovery of calculus was the result of many prior contributions from figures like Galileo, Kepler, Fermat, and others who studied the behavior of changing magnitudes.
• 😀 Ancient Greek mathematicians, particularly Archimedes, worked on approximating areas of curved shapes, using the method of exhaustion, which closely foreshadowed the idea of integration.
• 😀 Newton's contribution to calculus focused on rates of change, leading to the concept of the derivative, which he referred to as 'the method of fluxions.'
• 😀 Leibniz developed a method of integrating areas under curves, which was more generalized and ultimately became the more widely accepted notation, including the use of the integral symbol.
• 😀 Both Newton and Leibniz discovered the profound connection between differentiation and integration, understanding them as inverse operations.
• 😀 Newton's work was highly secretive, and he kept his findings on calculus to himself for 30 years, only revealing them after much delay, leading to a dispute with Leibniz over priority.
• 😀 Archimedes, using geometric methods, calculated the area under a parabola, which was later confirmed through integral calculus, showcasing the superiority of the calculus approach.
• 😀 The two forms of calculus, developed by Newton and Leibniz, solve problems like determining areas, velocities, and accelerations, which have wide applications in physics and engineering.
• 😀 Despite the controversies, the calculus of Newton and Leibniz became foundational for modern mathematics, enabling advances in multiple scientific fields, including mechanics, astronomy, and economics.

Q & A

What was the historical significance of Isaac Newton's discovery of calculus?

Isaac Newton's discovery of calculus revolutionized mathematics and science. His work on the concept of derivatives and integrals paved the way for advances in physics, particularly in understanding motion and forces. It helped lay the foundation for modern calculus and contributed to key theories, such as the law of universal gravitation.

How did Isaac Newton's background influence his contributions to science?

Isaac Newton came from a modest farming background, which played a key role in his determination to excel. Despite being somewhat of an outsider in his family, he showed a deep interest in science, leading him to develop groundbreaking theories. His upbringing highlighted his resilience and drive to make scientific advancements, regardless of his humble beginnings.

What was the relationship between Isaac Newton and Gottfried Wilhelm Leibniz regarding calculus?

Newton and Leibniz both independently developed calculus, but they had different approaches. While Newton developed his 'method of fluxions,' Leibniz focused on integrating functions through a different approach. The rivalry between the two became infamous, with both claiming priority over the discovery. Despite this, both contributed significantly to the field of calculus.

What role did earlier scientists like Galileo, Kepler, and Fermat play in the development of calculus?

Galileo, Kepler, Fermat, and others laid the groundwork for calculus by exploring concepts of velocity, acceleration, and the behavior of changing quantities. Galileo and Kepler's work on motion and Fermat's method for finding maxima and minima in functions were foundational. Their insights set the stage for later discoveries by Newton and Leibniz.

How did the ancient Greeks contribute to the development of calculus?

The ancient Greeks, particularly through mathematicians like Archimedes, made early attempts to solve geometric problems like finding the area under curves. Their method of exhaustion, which approximated areas using polygons, was a precursor to the integral calculus developed much later. Archimedes, in particular, calculated areas of segments of parabolas, which influenced later developments in calculus.

What was the significance of the 'method of exhaustion' used by the Greeks?

The method of exhaustion was an ancient Greek technique used to find the area of curved shapes. It involved approximating the area by inscribing polygons within the curve and increasing the number of sides until the approximation was close enough. This concept of limits foreshadowed integral calculus and is seen as an important early step towards the development of calculus.

Why did Isaac Newton keep his discoveries about calculus secret for many years?

Newton kept his discoveries about calculus secret for nearly 30 years due to his fear of criticism and a possible challenge to his work. He was deeply concerned about intellectual theft and his own reputation. His reluctance to publish his findings until later contributed to the controversy with Leibniz, who published his version of calculus earlier.

What was the 'fundamental theorem of calculus' and why was it important?

The fundamental theorem of calculus links differentiation and integration, showing that they are inverse operations. It states that the integral of a function can be used to recover its derivative. This theorem is crucial because it allows the calculation of areas and the study of rates of change, forming the backbone of modern calculus applications in science and engineering.

What was the controversy surrounding the priority of calculus between Newton and Leibniz?

The controversy over the priority of calculus centered on who first developed the concept. Newton had a head start, but Leibniz published his work first, which led to accusations of plagiarism. Both sides engaged in a bitter intellectual battle, with each claiming to have been the first to discover calculus. This rivalry caused lasting tension in the scientific community.

How did the work of Newton and Leibniz impact the world of mathematics and science?

The work of Newton and Leibniz fundamentally transformed mathematics and science. Their independent discoveries of calculus enabled the development of many branches of physics, engineering, and economics. Calculus became the language of science, essential for modeling change, motion, and other dynamic processes, laying the foundation for advancements in various fields, including space exploration, economics, and technology.