Sudut Dalam dan Sudut Luar Segitiga (Matematika SMP kelas 7)
Summary
TLDRIn this lesson, students explore the properties of triangles, focusing on the sum of interior and exterior angles. The teacher demonstrates how the sum of the interior angles of a triangle is always 180°, using various examples. The lesson also covers the relationship between exterior angles and the interior angles of a triangle, illustrating how the exterior angle equals the sum of the two non-adjacent interior angles. Several example problems are solved, including those involving angle sums and properties of isosceles triangles. The lesson concludes with a series of practice problems to reinforce the concepts.
Takeaways
- 😀 The sum of the interior angles of a triangle is always 180°.
- 😀 When the interior angles of a triangle are placed together, they form a straight angle (180°).
- 😀 Example: If two angles in a triangle are 75° and 65°, the third angle can be found by subtracting their sum from 180° (40°).
- 😀 The angles of a triangle can be in a ratio, such as 4:3:5, which allows you to find each angle using the equation 4A + 3A + 5A = 180°.
- 😀 A triangle with angles 60°, 45°, and 75° is an acute triangle because all angles are less than 90°.
- 😀 Exterior angles of a triangle are formed when one side is extended, and their relationship with interior angles is key.
- 😀 The exterior angle of a triangle is equal to the sum of the two non-adjacent interior angles.
- 😀 Example: In triangle ABC, extending side AB forms an exterior angle that is the sum of angles A and C.
- 😀 Another exterior angle formed by extending side BC is the sum of angles B and C.
- 😀 In triangle PQR, if it is an isosceles triangle, the base angles are equal. For example, if angle P equals angle R, their sum will help find the other angles.
Q & A
What is the sum of the interior angles of a triangle?
-The sum of the interior angles of any triangle is always 180°.
How can we prove that the sum of the interior angles of a triangle is 180°?
-We can prove it by placing the interior angles of a triangle (labeled as a, b, and c) on a straight angle (180°). By aligning the angles to form a straight line, we observe that the sum of the three angles equals 180°.
In the given example, how did they find the value of angle B?
-In the example, it was given that two angles were 75° and 65°. The sum of these angles was subtracted from 180°, resulting in 40° for angle B.
What is the relationship between the angles in a triangle when the angles are in the ratio 4:3:5?
-When the angles are in the ratio 4:3:5, we represent the angles as 4A, 3A, and 5A. Solving the equation 4A + 3A + 5A = 180° gives A = 15°. Therefore, the individual angles are 60°, 45°, and 75°.
What type of triangle is formed when all the interior angles are less than 90°?
-When all the interior angles are less than 90°, the triangle is classified as an acute triangle.
What is the definition of an exterior angle of a triangle?
-An exterior angle of a triangle is formed when a side of the triangle is extended. The angle formed outside the triangle is the exterior angle.
How do we find the value of an exterior angle based on the interior angles?
-An exterior angle is equal to the sum of the two non-adjacent interior angles. For example, if angle A and angle C are inside the triangle, the exterior angle at vertex B is equal to A + C.
In the second exterior angle example, what relationship was used to find the exterior angle?
-The relationship used was that the exterior angle at vertex B (angle CBD) is equal to the sum of the two opposite interior angles (angle A + angle C).
How can we calculate the interior angles of an isosceles triangle?
-In an isosceles triangle, the two base angles are equal. For example, if the sum of these two angles is 112°, then each of the base angles is 56°.
How do you solve for an unknown angle in a triangle if the sum of two known angles is provided?
-To solve for an unknown angle, subtract the sum of the known angles from 180°. For example, if the sum of two angles is 105°, then the unknown angle is 180° - 105° = 75°.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
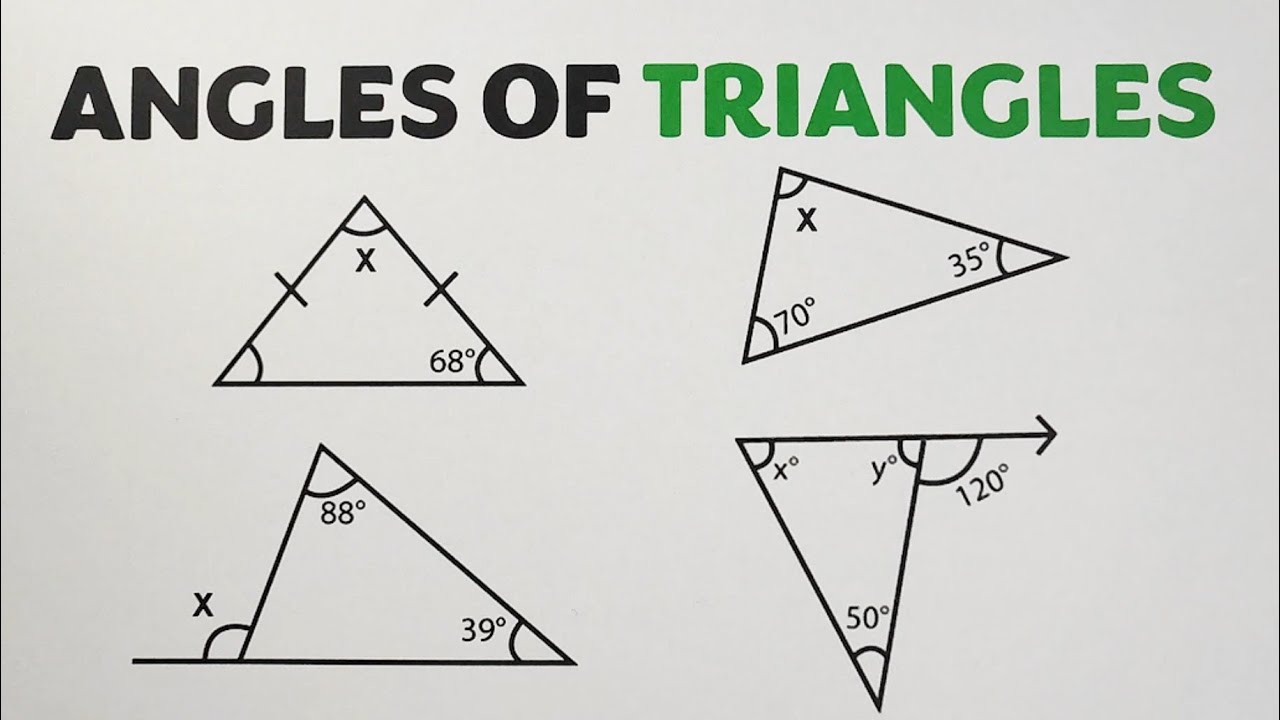
Angles of Triangle: Sum of Interior Angles and Exterior Angle Theorem by @MathTeacherGon
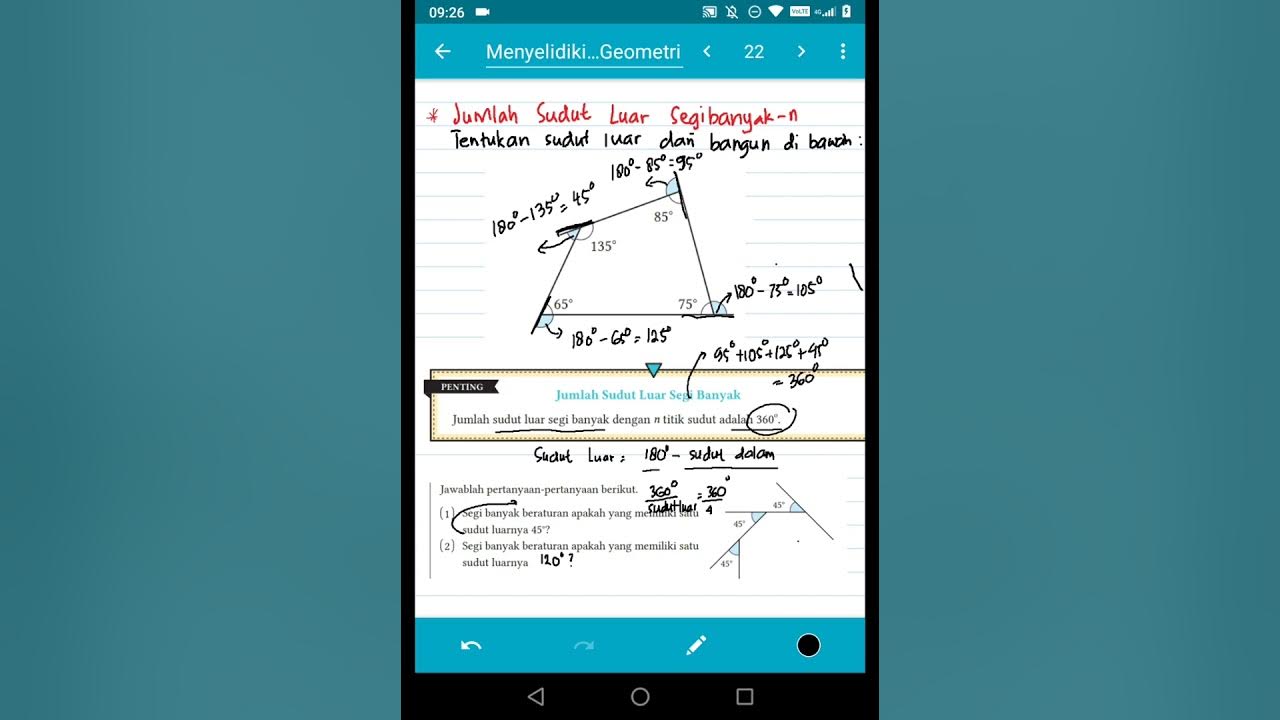
Sudut Luar Segibanyak-n

Interior and Exterior angles of polygons

Pembahasan Mari Kita Periksa Garis Sejajar dan Segi Banyak Hal 115 Bab 4 Kelas 8 Kurikulum Merdeka

Matematika Kelas 8 Bab 4 - Sudut Dalam Segi Banyak - hal. 110 - 112 - Kurikulum Merdeka

Matematika Kelas 8 Bab 4 - Sudut Luar Segi Banyak - hal. 113 - 114 - Kurikulum Merdeka
5.0 / 5 (0 votes)
