Penjumlahan dan Pengurangan Sudut
Summary
TLDRIn this educational video, the presenter explains the process of adding and subtracting angles in the degrees, minutes, and seconds format. The video demonstrates step-by-step how to align and sum up angles, ensuring proper conversion when values exceed 60 (such as converting seconds over 60 into minutes). It also covers how to borrow from the minutes and degrees when subtracting angles. Throughout, the presenter uses clear examples to illustrate the calculations, making the concepts accessible to viewers. By the end of the video, learners will be able to confidently handle angular arithmetic.
Takeaways
- 😀 The video focuses on teaching the addition and subtraction of angles and parallel lines.
- 😀 Viewers are reminded to subscribe to the channel, 'Pojok Matematika', before starting the lesson.
- 😀 The first step in adding and subtracting angles is to align the numbers by degrees, minutes, and seconds.
- 😀 The principle of borrowing is applied when values exceed the standard 59 for minutes or seconds.
- 😀 In the example, 32° 45' 54'' is added to 17° 50' 42'', with adjustments made to simplify values over 59.
- 😀 When minutes or seconds exceed 59, the extra values are converted to the next higher unit (minutes for seconds, degrees for minutes).
- 😀 A similar process is applied when subtracting angles, such as borrowing from the next unit when necessary.
- 😀 The lesson covers multiple examples, including subtraction where borrowing from both minutes and degrees is required.
- 😀 Viewers are shown how to break down complex values into degrees, minutes, and seconds before performing arithmetic.
- 😀 The video emphasizes the importance of ensuring that the final values are simplified and presented in standard angle format (degrees, minutes, seconds).
Q & A
What is the main topic of the video?
-The main topic of the video is the addition and subtraction of angles, specifically working with degrees, minutes, and seconds.
Why is it important to align the units (degrees, minutes, and seconds) correctly before performing calculations?
-It is important to align the units correctly to ensure the calculations are accurate. Degrees should be added with degrees, minutes with minutes, and seconds with seconds.
What should you do if the sum of the seconds or minutes exceeds 59?
-If the sum of the seconds or minutes exceeds 59, you need to convert 60 seconds into 1 minute, and 60 minutes into 1 degree, then adjust the result accordingly.
How do you handle borrowing in angle subtraction?
-When borrowing in angle subtraction, you convert the lower unit into a higher unit. For example, if the seconds are smaller than what is needed, you borrow from the minutes, and if minutes are insufficient, you borrow from the degrees.
What happens when subtracting 31 seconds from 55 seconds?
-Since 31 is smaller than 55, you borrow 1 minute (which is 60 seconds), converting the 31 seconds to 91 seconds, allowing for the subtraction to proceed.
What is the process to simplify the sum of 96 minutes in the example given?
-When you have 96 minutes, you convert 60 minutes into 1 degree, and then add the remaining 36 minutes to the total. This gives a simplified result.
How do you handle the conversion of degrees, minutes, and seconds when performing calculations?
-You first convert any fractional degrees into minutes (by multiplying by 60), then convert any fractional minutes into seconds (by multiplying by 60), ensuring all units are in the proper form before performing the addition or subtraction.
What should you do if the minutes exceed 59 in the sum or difference of angles?
-If the minutes exceed 59, you should convert 60 minutes into 1 degree and add it to the degrees, then adjust the minutes accordingly.
What is the result when adding 50° 7' 12'' and 17° 53' 53''?
-The result of adding these angles is 67° 60' 65''. After adjusting for the excess minutes and seconds, the final result becomes 68° 12'.
In the subtraction example, why is it necessary to borrow from the degrees when the minutes are insufficient?
-It is necessary to borrow from the degrees because when subtracting angles, if the minutes of the smaller angle are greater than the minutes of the larger angle, you need to borrow a degree to complete the subtraction.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
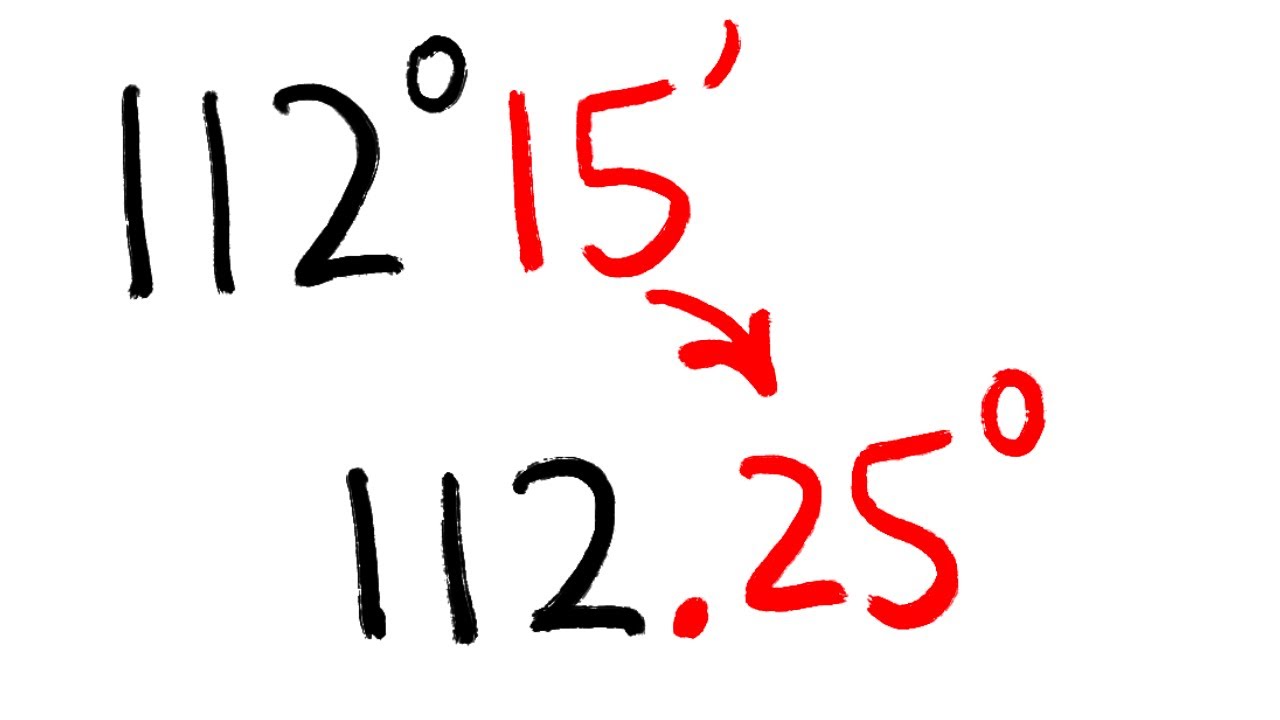
Convert degrees, minutes, and seconds (dms) into decimal degrees

Konversi Sudut - Ukuran Derajat - Konversi Radian ke Derajat dan Sebaliknya - Trigonometri Part 3

Ángulo en grados sexagesimales

ANGLES IN A UNIT CIRCLE || PRE-CALCULUS

CARA MENGUBAH KOORDINAT DMS KE DD

Garis dan Sudut (2) | Satuan Sudut | Matematika Kelas 7
5.0 / 5 (0 votes)
