Grafik dan Nilai Mutlak Bilangan Kompleks
Summary
TLDRIn this educational video, Dwi Anggraini explains the concept of complex numbers, starting with the basics of their structure—combining real and imaginary numbers. She elaborates on representing complex numbers graphically on the Cartesian plane, with real and imaginary axes, and how to calculate the modulus of a complex number. The video also covers vector-based operations like addition and subtraction of complex numbers, illustrated with practical examples. Viewers are introduced to key mathematical concepts like the modulus and how to visualize and calculate complex number operations, setting the stage for further study in polar and exponential forms.
Takeaways
- 😀 Introduction to complex numbers as a combination of real and imaginary numbers (a + bi).
- 😀 Imaginary numbers are numbers that, when squared, result in a negative value, commonly represented as √-1.
- 😀 Complex numbers can be represented as coordinates on the Cartesian plane, where the x-axis is the real axis and the y-axis is the imaginary axis.
- 😀 A complex number can be expressed as a point (x, y) on the complex plane, where 'x' is the real part and 'y' is the imaginary part.
- 😀 The modulus or absolute value of a complex number can be calculated using the distance formula between the point and the origin (0,0).
- 😀 The modulus of a complex number z = x + yi is √(x² + y²), where x and y are the real and imaginary components.
- 😀 A complex number can also be expressed as a vector, where the direction and magnitude of the vector represent the complex number.
- 😀 Addition and subtraction of complex numbers can be done using vectors, visualized on the complex plane as operations on the points corresponding to the complex numbers.
- 😀 For addition, vectors representing complex numbers can form a parallelogram, and the sum corresponds to the diagonal of this parallelogram.
- 😀 For subtraction, the difference of two complex numbers can be calculated by subtracting their corresponding coordinates and visualizing the operation on the complex plane.
- 😀 The video ends with a teaser for the next topic: polar and exponential forms of complex numbers, encouraging viewers to subscribe and stay updated.
Q & A
What is a complex number?
-A complex number consists of a real part and an imaginary part. It is expressed as Z = a + bi, where 'a' is the real part and 'b' is the imaginary part, with 'i' representing the imaginary unit (√-1).
How can complex numbers be represented graphically?
-Complex numbers can be represented as points on the Cartesian coordinate plane, where the x-axis represents the real part and the y-axis represents the imaginary part.
What is the modulus or absolute value of a complex number?
-The modulus (or absolute value) of a complex number is the distance from the origin (0, 0) on the complex plane, calculated as |Z| = √(x² + y²), where x and y are the real and imaginary parts, respectively.
Can you give an example of a complex number and its modulus?
-For the complex number Z = 2 + 2i, the modulus is calculated as |Z| = √(2² + 2²) = √8 = 2√2.
What is the significance of the imaginary unit 'i' in complex numbers?
-The imaginary unit 'i' represents the square root of -1. It is a fundamental concept in complex numbers, as it allows for the representation of numbers that cannot be expressed as real numbers.
How are complex numbers added or subtracted graphically?
-Complex numbers can be added or subtracted using vectors. The graphical representation involves combining the vectors head-to-tail for addition or reversing the direction for subtraction.
What is the rule for adding complex numbers in vector form?
-To add complex numbers in vector form, you add their real and imaginary parts separately. This can be visualized by creating a parallelogram or using the head-to-tail method.
How do you subtract complex numbers using vectors?
-Subtraction of complex numbers in vector form involves subtracting the corresponding real and imaginary components. This can be visualized by reversing the direction of one of the vectors and then adding the two vectors.
What is the result of adding two complex numbers, 2 + 4i and 4 + i?
-The sum of 2 + 4i and 4 + i is 6 + 5i, obtained by adding the real parts (2 + 4) and the imaginary parts (4i + i) separately.
What is the focus of the next video in the series?
-The next video will cover the polar and exponential forms of complex numbers, providing a deeper understanding of their different representations.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Complex Numbers 01 | Introduction to Complex Numbers | Class 11 | JEE

Prereq 13: Complex Numbers

APA ITU BILANGAN KOMPLEKS ? (Materi Kurikulum Merdeka)

LATIHAN A NO 1 2 3 BILANGAN KOMPLEKS MATEMATIKA TINGKAT LANJUT SMA KELAS 11 #kurikulummerdeka

COMPLEXOS: OPERAÇÕES NA FORMA ALGÉBRICA (+, -, X) (AULA 4/14)
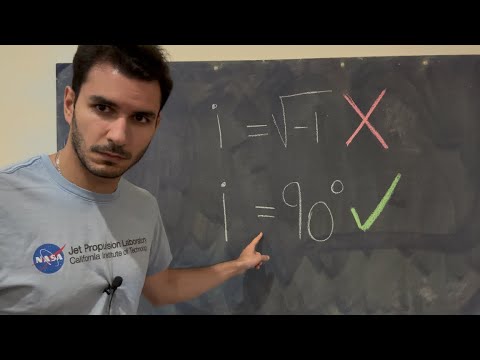
Imaginary numbers aren't imaginary
5.0 / 5 (0 votes)
