Demostración del teorema de Pitágoras
Summary
TLDREn este video, se realiza una demostración geométrica del teorema de Pitágoras, explicando cómo el cuadrado de la hipotenusa en un triángulo rectángulo es igual a la suma de los cuadrados de los catetos. Se utiliza un enfoque visual con triángulos rectángulos y cuadrados para ilustrar cómo se forma esta relación, destacando la importancia de los catetos y la hipotenusa. Se muestra cómo la superficie de un cuadrado formado por los triángulos es igual a la suma de los cuadrados de los catetos y el cuadrado de la hipotenusa, demostrando así el teorema de manera clara y accesible.
Please replace the link and try again.
Q & A
¿Qué establece el teorema de Pitágoras?
-El teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
¿Cómo se reconoce la hipotenusa en un triángulo rectángulo?
-La hipotenusa es el lado más largo del triángulo rectángulo, y es el que está opuesto al ángulo de 90 grados.
¿Qué se construye al principio del ejercicio geométrico?
-Se construye un cuadrado utilizando cuatro triángulos rectángulos idénticos, cuyos catetos son 'a' y 'b'.
¿Por qué se utiliza un cuadrado en la demostración?
-El cuadrado se utiliza para visualizar cómo las áreas de los triángulos y sus catetos se relacionan con la hipotenusa y cómo se puede demostrar el teorema de Pitágoras de manera geométrica.
¿Qué representan los catetos 'a' y 'b' en el triángulo rectángulo?
-Los catetos 'a' y 'b' son los dos lados más cortos del triángulo rectángulo, mientras que la hipotenusa es el lado largo.
¿Cómo se muestra que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa?
-Se muestra reordenando los triángulos y organizándolos dentro de un cuadrado grande, de modo que el área del cuadrado formado por la hipotenusa es igual a la suma de los cuadrados de los catetos.
¿Qué importancia tiene el concepto del ángulo de 90 grados en el triángulo rectángulo?
-El ángulo de 90 grados es crucial porque identifica el triángulo como rectángulo, lo que permite aplicar el teorema de Pitágoras para calcular las longitudes de los lados.
¿Cómo se reorganizan los triángulos en la demostración geométrica?
-Los triángulos se reorganizan para colocar los cuadrados de los catetos dentro de un espacio que originalmente estaba ocupado por el cuadrado de la hipotenusa, evidenciando así que ambas áreas son iguales.
¿Qué se deduce al final de la demostración?
-Se deduce que el área del cuadrado de la hipotenusa es igual a la suma de las áreas de los cuadrados de los catetos, lo que confirma el teorema de Pitágoras.
¿Por qué es importante la comprensión visual del teorema de Pitágoras?
-La comprensión visual ayuda a entender cómo las áreas de las figuras se interrelacionan, haciendo más clara la relación matemática que expresa el teorema de Pitágoras.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Teorema de Pitágoras - MasterD
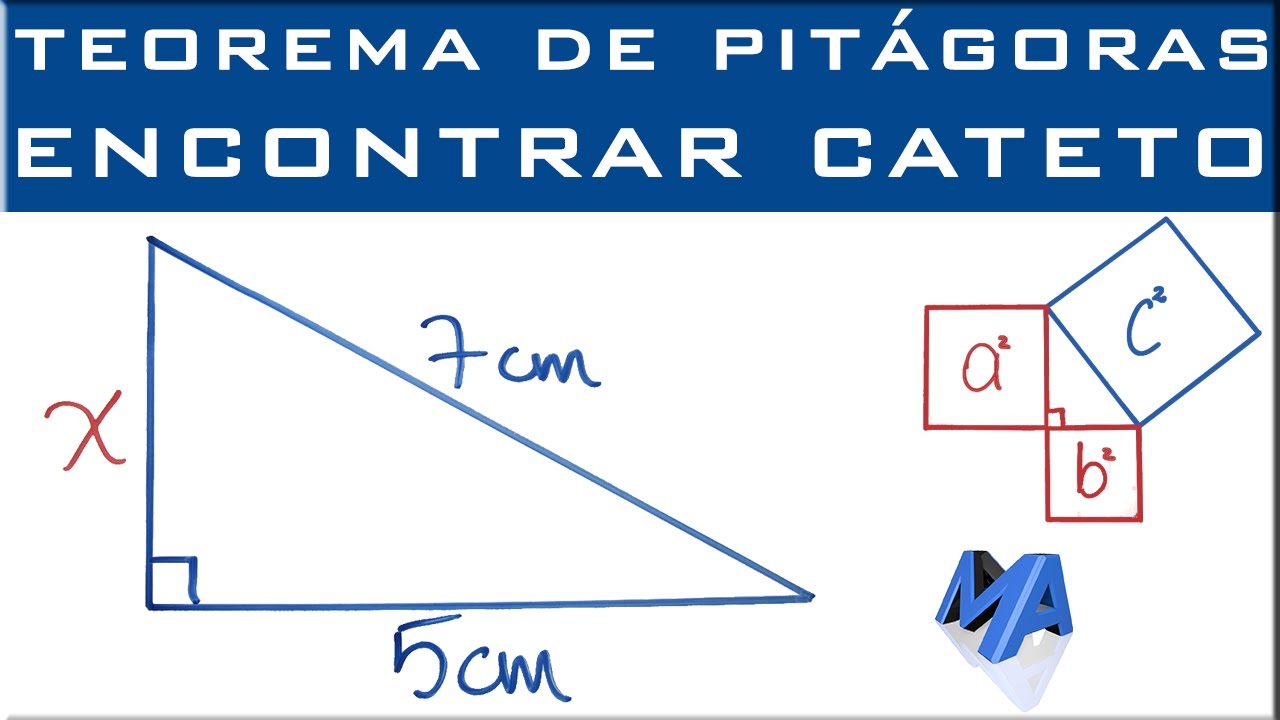
Teorema de Pitágoras | Encontrar un cateto
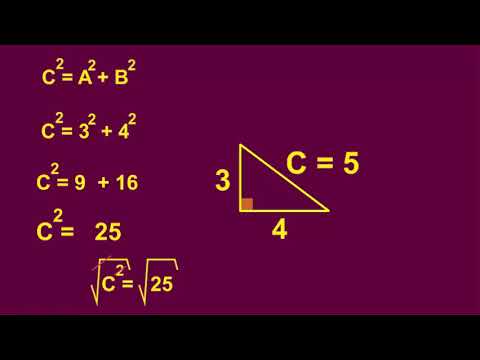
TEOREMA DE PITÁGORAS y su verificación gráfica, en solo dos minutos

Distancia entre dos puntos, usando Teorema de Pitágoras

Teorema de Pitágoras Introducción
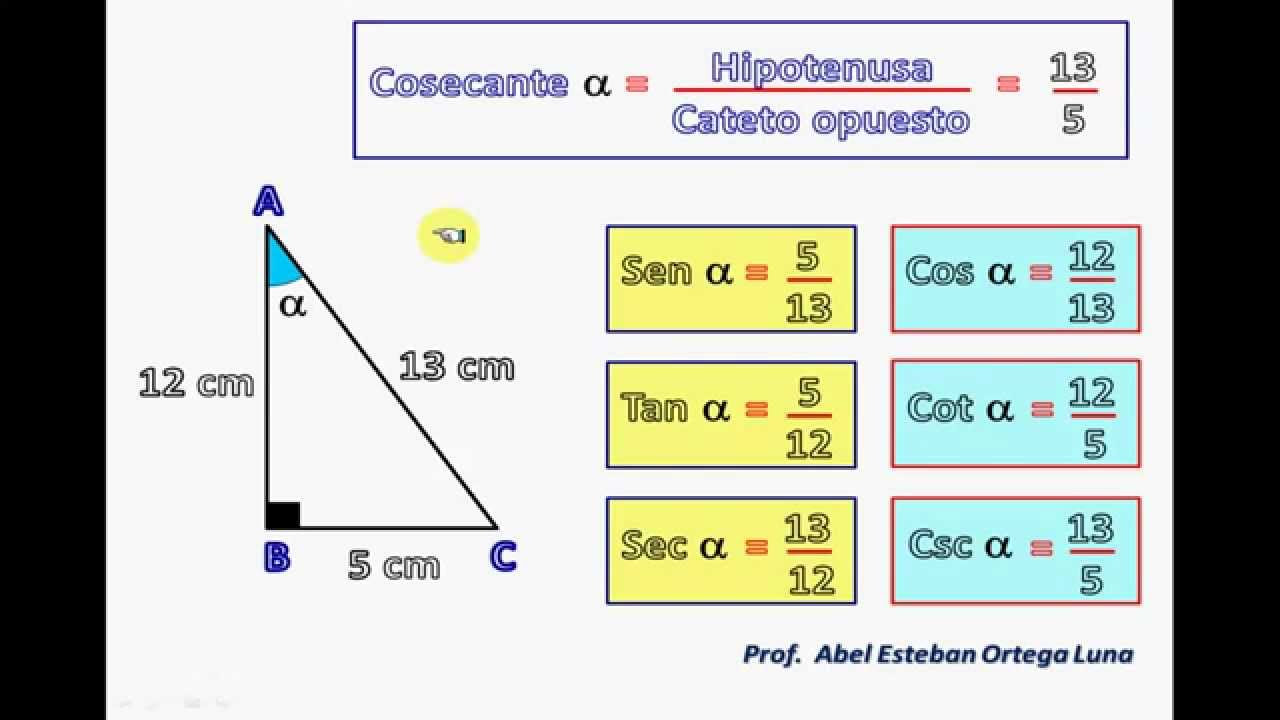
RAZONES TRIGONOMÉTRICAS EN UN TRIÁNGULO RECTÁNGULO

Distancia entre dos puntos ejemplo 3 método gráfico
5.0 / 5 (0 votes)