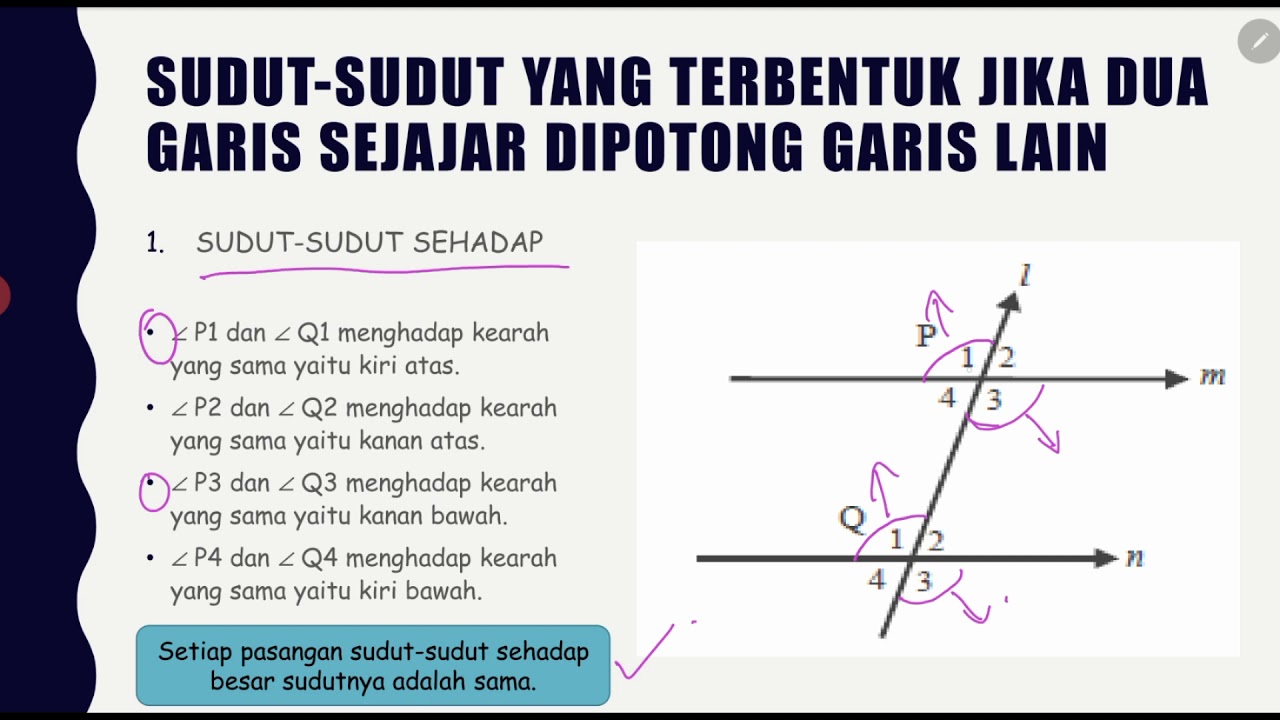
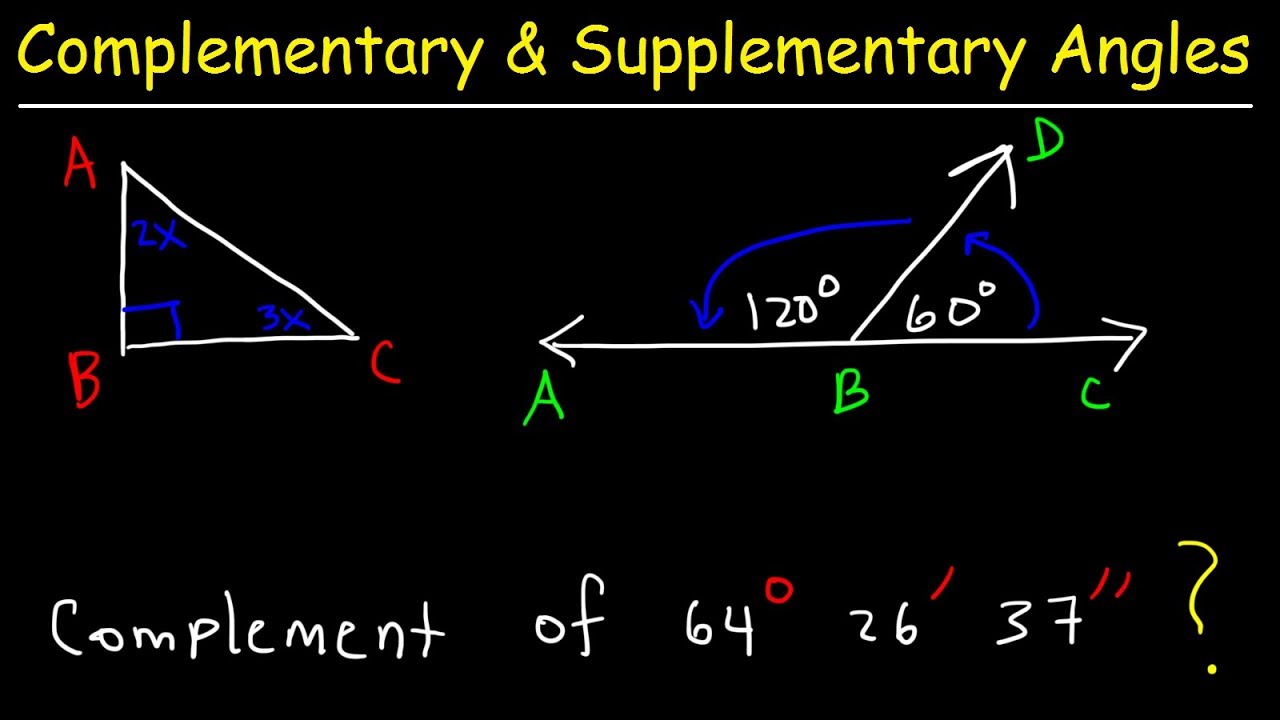
HUBUNGAN ANTAR SUDUT (Berpelurus, Berpenyiku, Bertolak Belakang) Kelas 7 SMP

Summary

In this educational video, Pak Beni explains various relationships between angles, starting with complementary angles that sum up to 180°. He then covers right angles that sum up to 90° and discusses opposite angles, which are always equal. Through examples, Pak Beni demonstrates how to calculate angle values using algebra and simple geometric principles. The video aims to help viewers understand angle relationships, offering step-by-step instructions and problem-solving strategies. It concludes with a reminder to like, share, and subscribe for further lessons.

Takeaways

• 😀 Understanding supplementary angles: Two angles are supplementary when their sum equals 180°.
• 😀 Right angles: Two angles are perpendicular if their sum equals 90°, forming a right angle.
• 😀 The relationship between opposite angles: Opposite angles are always equal in size.
• 😀 Example of calculating supplementary angles: When two angles sum to 180°, use subtraction to find the unknown angle.
• 😀 Using algebra to solve for angles: If given algebraic expressions for angles, set up an equation to find the unknown variable.
• 😀 Concept of complementary angles: Two angles are complementary when they sum to 90°.
• 😀 Calculating angles with algebra: For equations involving unknowns, solve for the variable by isolating it on one side.
• 😀 The importance of knowing angle symbols: The symbol for 90° is a box (□) and represents a right angle.
• 😀 Practical problem-solving: Apply angle relationships to find unknown angles, whether using known values or algebraic expressions.
• 😀 The connection between angles and geometry: Each angle relationship (supplementary, complementary, opposite) forms the basis for solving geometry problems.

Q & A

What is meant by 'angles that are supplementary'?

Supplementary angles are two angles that together form a straight line, totaling 180 degrees. One angle is the supplement of the other.

How can you calculate the value of an unknown angle when two angles are supplementary?

To find an unknown angle, you subtract the known angles from 180°. For example, if one angle is 38° and the other is 90°, you subtract both from 180° to find the unknown angle.

What is the relationship between angles that form a right angle (90°)?

Angles that form a right angle are called complementary angles. The sum of these angles is always 90°.

How do you calculate the value of an unknown angle when two angles are complementary?

To find the value of an unknown complementary angle, subtract the known angle from 90°. For example, if one angle is 45°, the other angle is 90° - 45° = 45°.

How does algebra come into play in solving supplementary angles?

In problems involving supplementary angles and algebra, you can represent angles using variables and solve equations. For example, if an angle is 3x + 15° and another is 2x + 10°, you set up an equation where their sum equals 180° and solve for x.

What is the result of solving for x in a supplementary angle problem like 3x + 15° and 2x + 10°?

By simplifying the equation and solving for x, you find that x = 31°.

What are opposite (vertical) angles, and how are they related?

Opposite or vertical angles are two angles formed when two lines intersect. These angles are always equal in size. For example, if one angle is 120°, the opposite angle will also be 120°.

How do you find the value of an unknown angle in a vertical angle problem?

To find the value of an unknown angle in a vertical angle problem, simply set the opposite angles equal to each other and solve for the variable.

How do you solve a vertical angle equation like 2x = 120°?

To solve for x, divide both sides of the equation by 2. In this case, x = 120° / 2 = 60°.

What is the final recap of the three main relationships of angles covered in the video?

The three main angle relationships covered in the video are: supplementary angles, which total 180°; complementary angles, which total 90°; and vertical angles, which are always equal in size.