Intervalos de números reales

Summary

En este video se explica el concepto de intervalos en matemáticas, abordando su definición como subconjuntos de los números reales. Se presentan diferentes tipos de intervalos: acotados y no acotados, y se profundiza en la notación para escribirlos, tanto en pares como en desigualdad. Además, se explica la clasificación de intervalos en abiertos, cerrados y semiabiertos, detallando cómo se representan en notación matemática. El video también incluye ejemplos prácticos para identificar y clasificar intervalos, finalizando con una invitación a compartir el contenido.

Takeaways

• 😀 Los intervalos son subconjuntos de los números reales, que pueden ser acotados o no acotados.
• 😀 Los intervalos acotados tienen límites en ambos lados, mientras que los no acotados no tienen límites en uno o ambos lados.
• 😀 La notación de intervalos puede escribirse en dos formas principales: notación en pares y notación en desigualdad.
• 😀 En la notación de pares, los números que delimitan el intervalo se colocan entre paréntesis o corchetes, dependiendo del tipo de intervalo.
• 😀 Los intervalos en notación de desigualdad utilizan los signos de menor que (<) y mayor que (>) para indicar los valores que conforman el intervalo.
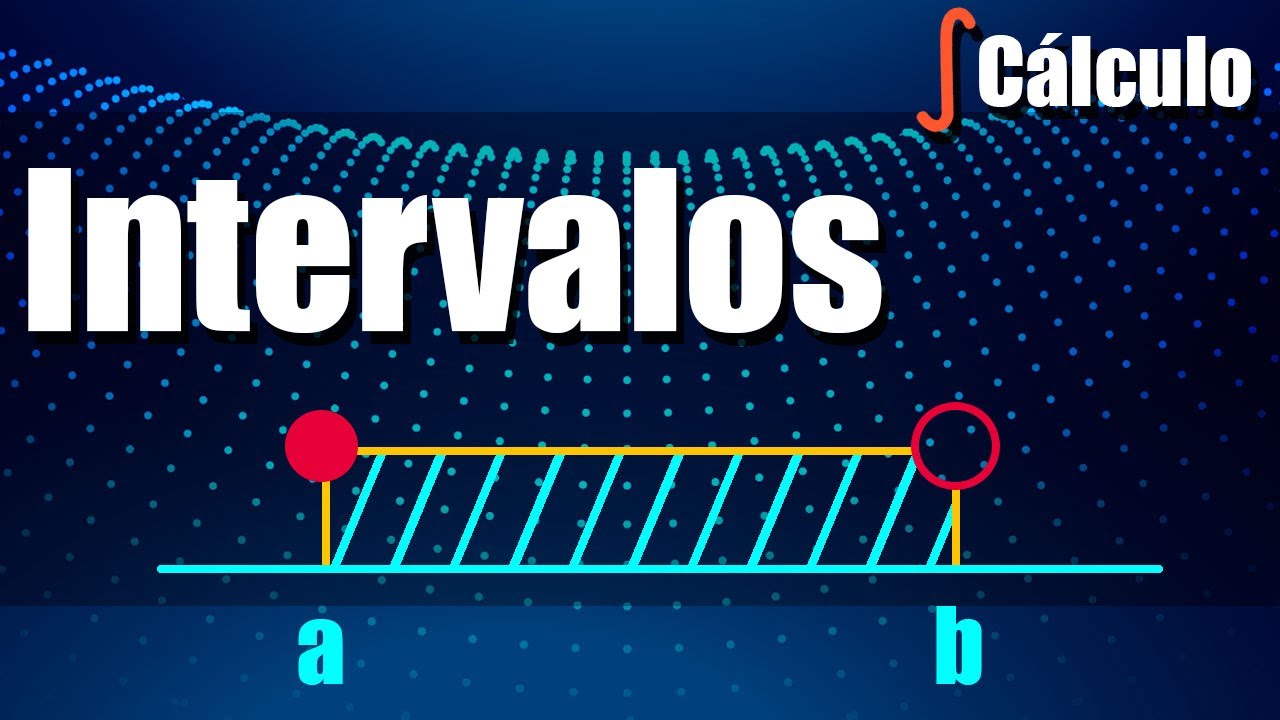
• 😀 Un intervalo abierto no incluye sus extremos. Por ejemplo, el intervalo (-1, 7) no incluye -1 ni 7.
• 😀 Los intervalos cerrados incluyen sus extremos. En la notación de pares, se usan corchetes para denotar intervalos cerrados, como [-1, 7].
• 😀 Los intervalos semiabiertos (o mixtos) incluyen uno de los extremos pero no el otro. Ejemplo: [3, 9) incluye 3 pero no 9.
• 😀 El uso de paréntesis en la notación de pares indica un intervalo abierto, mientras que los corchetes indican un intervalo cerrado.
• 😀 En la práctica, los intervalos pueden ser identificados mediante ejemplos, determinando si son abiertos, cerrados o mixtos, basándose en su notación.

Q & A

¿Qué es un intervalo en matemáticas?

Un intervalo es un subconjunto de los números reales (R), que puede ser acotado o no acotado, y se utiliza para representar conjuntos de números entre dos límites.

¿Qué significa que un intervalo sea acotado?

Un intervalo es acotado cuando tiene límites definidos en ambos lados. Es decir, tiene un límite inferior y un límite superior.

¿Qué es un intervalo abierto?

Un intervalo abierto es aquel que no incluye sus extremos. Esto significa que los valores en los extremos no forman parte del conjunto.

¿Cómo se representa un intervalo abierto?

En notación de pares, un intervalo abierto se representa con paréntesis. Por ejemplo, (-1, 7) indica todos los números reales entre -1 y 7, excluyendo esos dos valores.

¿Qué es un intervalo cerrado?

Un intervalo cerrado incluye ambos extremos. Es decir, los valores en los límites inferior y superior también forman parte del conjunto.

¿Cómo se representa un intervalo cerrado?

En notación de pares, un intervalo cerrado se representa con corchetes. Por ejemplo, [-1, 7] incluye los números -1 y 7, además de todos los números entre ellos.

¿Qué es un intervalo semiabierto o mixto?

Un intervalo semiabierto o mixto es aquel que incluye uno de sus extremos, pero no el otro. Por ejemplo, [3, 9) incluye 3, pero no 9.

¿Cómo se representa un intervalo semiabierto o mixto?

En notación de pares, un intervalo semiabierto se representa con corchetes en un extremo y paréntesis en el otro. Por ejemplo, [3, 9) o (3, 9].

¿Qué significa que un intervalo sea acotado por ambos lados?

Un intervalo acotado por ambos lados significa que tiene límites definidos en los dos extremos, es decir, tiene un límite inferior y uno superior, y ambos son parte del intervalo.

En el ejemplo dado, ¿qué tipo de intervalo es (-2, 4)?

El intervalo (-2, 4) es un intervalo abierto porque no incluye los extremos -2 y 4, representado por los paréntesis.