Cross products | Chapter 10, Essence of linear algebra
Summary
TLDRThis video script delves into the concept of cross products, starting with a basic introduction for two-dimensional vectors by visualizing the parallelogram formed and explaining how orientation affects the sign of the cross product. It emphasizes the importance of determinants in calculating the area of this parallelogram, which serves as the magnitude of the cross product. The script then transitions to the true three-dimensional cross product, where a new vector is derived, perpendicular to the original vectors, with magnitude equal to the parallelogram's area and direction determined by the right-hand rule. The video promises a deeper exploration of the cross product's geometric and linear transformational significance in a follow-up video, hinting at the elegance of the underlying mathematical concepts.
Takeaways
- 📚 The video script provides an introduction to the concept of the cross product, with a standard explanation and a deeper understanding in the context of linear transformations.
- 📏 The cross product is initially discussed in two dimensions, involving two vectors and the parallelogram they define.
- 📈 The cross product of two vectors v and w is related to the area of the parallelogram spanned by these vectors, with the sign depending on the orientation (v to the right of w gives a positive area, and vice versa).
- 🔄 The order of the vectors in the cross product matters; swapping them changes the sign of the result.
- 🧭 The orientation can be remembered using the right-hand rule, with the cross product of the basis vectors i-hat and j-hat being positive.
- 🔢 The determinant is used to calculate the cross product in 2D, by placing the vectors as columns in a matrix and computing the determinant.
- 📉 The determinant measures how areas change due to a transformation, which is why it's used to find the area of the parallelogram resulting from the transformation of a unit square.
- 📊 The cross product is not just a number but also a vector in 3D, with its magnitude being the area of the parallelogram and its direction perpendicular to the plane of the two original vectors.
- ✋ The right-hand rule is used to determine the direction of the cross product vector in 3D, ensuring it is perpendicular to both original vectors.
- 🔄 The script mentions a 3D determinant process for calculating the cross product, which involves a matrix with the basis vectors and the vectors being crossed.
- 🤔 The deeper understanding of the cross product in relation to linear transformations and the underlying geometry will be discussed in a follow-up video.
Q & A
What is the cross product of two vectors?
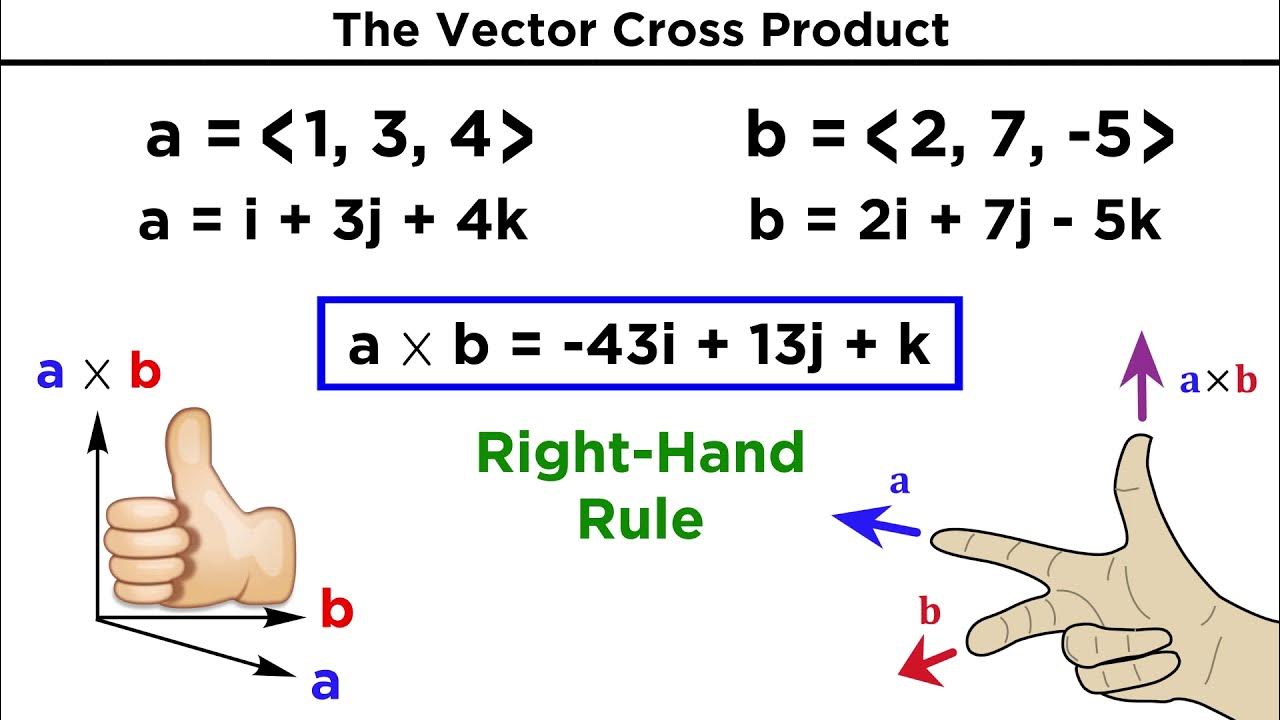
-The cross product of two vectors v and w is a vector that is perpendicular to both v and w, with a magnitude equal to the area of the parallelogram defined by v and w. Its direction is determined by the right-hand rule.
Why is the order of vectors important in the cross product?
-The order of vectors is important because it determines the orientation of the resulting cross product. If v cross w is positive, then v is on the right of w. If v is on the left of w, then v cross w is negative.
How does the orientation of vectors affect the cross product?
-The orientation affects the sign of the cross product. If the vectors are in a right-handed orientation (v on the right of w), the cross product is positive. If they are in a left-handed orientation (v on the left of w), the cross product is negative.
What is the relationship between the cross product and the determinant?
-The cross product can be computed using the determinant of a matrix where the columns represent the vectors being crossed. The determinant measures how areas change due to a transformation, and in the case of the cross product, it gives the area of the parallelogram formed by the vectors.
How can you remember the correct order for the cross product of the basis vectors i-hat and j-hat?
-You can remember the correct order by noting that the result of i-hat cross j-hat should be positive. Since i-hat is on the right of j-hat, v cross w should be positive when v is on the right of w.
What happens to the cross product if one of the vectors is scaled?
-If one of the vectors, say v, is scaled up by a factor of k (e.g., k*v), the cross product is also scaled up by that same factor. So, k*v cross w will be k times the value of v cross w.
What is the geometric interpretation of the cross product vector?
-The cross product vector geometrically represents a vector that is perpendicular to the plane containing the original vectors v and w. Its magnitude is equal to the area of the parallelogram spanned by v and w.
How does the right-hand rule help in determining the direction of the cross product?
-The right-hand rule helps in determining the direction of the cross product by pointing the forefinger of your right hand in the direction of vector v, and the middle finger in the direction of vector w. The direction of the thumb points in the direction of the cross product.
What is the significance of the parallelogram area in the cross product?
-The area of the parallelogram, which is spanned by the two vectors being crossed, is significant because it determines the magnitude of the cross product vector.
How is the cross product computed in three dimensions?
-In three dimensions, the cross product is computed using a 3x3 matrix where the first column contains the basis vectors i-hat, j-hat, and k-hat, and the second and third columns contain the coordinates of vectors v and w. The determinant of this matrix gives a linear combination of the basis vectors, which defines the cross product vector.
What is the connection between the cross product and linear transformations?
-The cross product is related to linear transformations through the determinant, which measures how areas change due to a transformation. The cross product vector is a result of such a transformation, where the original unit square is transformed into a parallelogram whose area is given by the determinant.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Dot vs. cross product | Physics | Khan Academy

Everything You Need to Know About VECTORS
The Vector Cross Product

Producto punto vs. producto cruz

3]Dot & Cross Product with Examples - Vector Analysis - GATE Engineering Mathematics
Vektor Matematika Kelas 10 • Part 2: Kesamaan Dua Vektor & Perkalian Vektor dengan Skalar
5.0 / 5 (0 votes)
