Percobaan, Ruang Sampel dan Kejadian ||Materi, Soal & Pembahasan||

Summary

This educational video explains the concept of sample spaces and events in probability, using various practical examples. Viewers learn about experiments such as tossing a coin, rolling a die, and drawing cards, where each experiment has a set of possible outcomes called the sample space. The video goes on to explain events as subsets of this sample space, with specific examples like odd numbers or sums of dice. Through tables and diagrams, the video demonstrates how to calculate the sample space and identify events, making the concepts accessible and engaging for learners.

Takeaways

• 😀 Percobaan (experiment) is any activity that results in several possible outcomes, like flipping a coin, rolling a die, or drawing a card.
• 😀 Sample space (ruang sampel) refers to the set of all possible outcomes of an experiment and is denoted by the letter 'S'.
• 😀 The number of elements in the sample space is called the number of sample points (NS), and these are represented within curly braces {}.
• 😀 A 'kejadian' (event) is a subset of the sample space, often denoted by capital letters like A, B, or C.
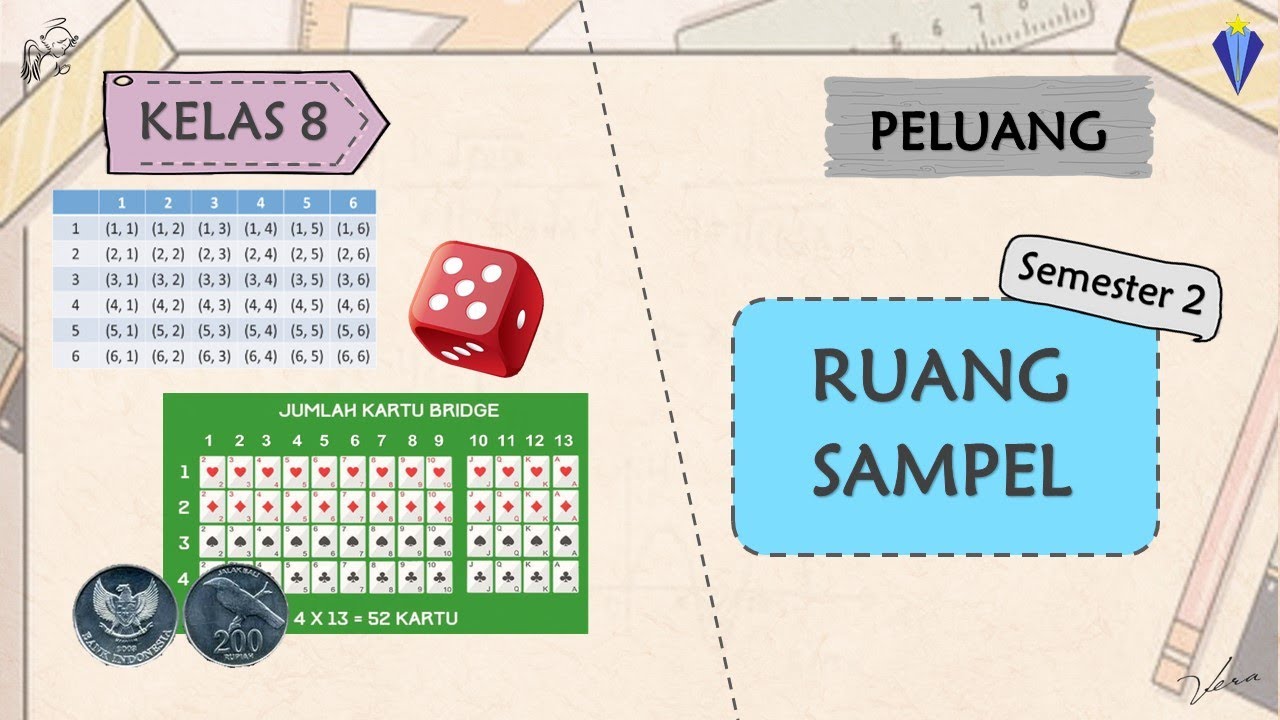
• 😀 Example: When rolling a die, the sample space is S = {1, 2, 3, 4, 5, 6} with 6 outcomes, or sample points.
• 😀 In a coin toss experiment, the sample space is S = {A, G} for 'angka' (heads) and 'gambar' (tails), with 2 possible outcomes.
• 😀 When both a die and a coin are tossed together, the sample space grows to S = {A1, A2, A3, A4, A5, A6, G1, G2, G3, G4, G5, G6} with 12 outcomes.
• 😀 Events can be specific combinations of outcomes from the sample space, like odd numbers on a die or a specific result in a coin toss.
• 😀 In the case of rolling two dice, the sample space includes all possible combinations from 1 to 6 for each die, resulting in 36 possible outcomes.
• 😀 When rolling two dice and looking for outcomes that sum to 9, the valid combinations are (3, 6), (4, 5), (5, 4), and (6, 3), giving 4 outcomes.
• 😀 Events can be defined by constraints, such as looking for outcomes where the sum of the dice is less than 7. This limits the valid combinations.
• 😀 For experiments involving multiple coins (like tossing three coins), a tree diagram is helpful in mapping all possible outcomes, with a specific event defined as having at least two heads.

Q & A

What is a sample space in the context of an experiment?

A sample space is the set of all possible outcomes of an experiment. It is denoted by the letter 'S'. For example, in a coin toss, the sample space is {Heads, Tails}.

What is an event in probability theory?

An event is a subset of the sample space, meaning it consists of one or more outcomes from the sample space. Events are typically denoted by capital letters like A, B, or C.

How do you denote the number of elements in a sample space?

The number of elements in a sample space is denoted by 'n(S)', where 'S' is the sample space. It represents the total count of all possible outcomes in the experiment.

What is the sample space for rolling a single die?

The sample space for rolling a single die is S = {1, 2, 3, 4, 5, 6}, since there are six faces on a die, each showing a different number.

What is the sample space when flipping a coin?

The sample space for flipping a coin is S = {H, G}, where 'H' stands for Heads and 'G' stands for Tails.

What is meant by 'complementary events' in probability?

Complementary events are two events that together cover the entire sample space. If event A occurs, the complement of A (denoted A') is the event where A does not occur. The probability of A plus the probability of A' is equal to 1.

In the example of throwing a die and tossing a coin, how many possible outcomes are there?

When throwing a die and tossing a coin together, the total number of possible outcomes is 12. This is because the die has 6 outcomes and the coin has 2 outcomes, so 6 * 2 = 12.

What is the probability of getting an odd number when rolling a die?

The odd numbers on a die are 1, 3, and 5. Therefore, the event of rolling an odd number consists of these three outcomes. The probability is 3 out of 6, or 1/2.

How do you calculate the sample space for the sum of two dice?

The sample space for the sum of two dice consists of all possible pairs of numbers (1,1), (1,2), (1,3), ..., (6,6). There are 36 total outcomes because each die has 6 faces, so 6 * 6 = 36.

What is the sample space when tossing 3 coins at once?

When tossing 3 coins, the sample space consists of all possible combinations of Heads (H) and Tails (T), represented as: {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}.