0625 Distribución binomial
Summary
TLDREste video explica detalladamente la distribución binomial, su función de probabilidad, y cómo calcular la esperanza y la varianza de una variable aleatoria binomial. A través de ejemplos, como la probabilidad de encontrar artículos defectuosos en una muestra, se ilustra la aplicación práctica de esta distribución en contextos reales. Se abordan conceptos clave como la fórmula binomial, el cálculo de probabilidades, y la demostración de propiedades como la esperanza (np) y la varianza (np(1-p)), proporcionando una comprensión clara de la distribución y su uso en la estadística.
Takeaways
- 😀 La distribución binomial modela el número de éxitos en una secuencia de ensayos Bernoulli independientes con probabilidad de éxito p.
- 😀 La variable aleatoria X en una distribución binomial puede tomar valores entre 0 y n, representando el número de éxitos en n ensayos.
- 😀 La función de probabilidad de la distribución binomial está dada por la fórmula: f(x) = C(n, x) * p^x * (1-p)^(n-x), donde C(n, x) es el coeficiente binomial.
- 😀 La probabilidad de obtener 0 éxitos (f(0)) es igual a (1-p)^n, mientras que la probabilidad de obtener n éxitos (f(n)) es igual a p^n.
- 😀 La esperanza (media) de una variable aleatoria binomial es E[X] = n * p, lo que representa el número promedio de éxitos.
- 😀 La varianza de una variable binomial es Var(X) = n * p * (1-p), lo que indica la dispersión de los resultados respecto a la media.
- 😀 La función generadora de probabilidades de la distribución binomial tiene la forma G(t) = (1 - p) + p * t^n.
- 😀 La esperanza y la varianza de la distribución binomial también se pueden derivar de la suma de variables aleatorias independientes con distribución Bernoulli.
- 😀 En una situación práctica, como el ejemplo con artículos defectuosos, se puede calcular la probabilidad de obtener al menos un éxito (artículo defectuoso) usando la fórmula de la distribución binomial.
- 😀 En el ejemplo con 100 artículos y una probabilidad de defectuosos de 7%, se encuentra que la probabilidad de que al menos uno de los 5 artículos seleccionados al azar sea defectuoso es 0.2639 o 26.39%.
Please replace the link and try again.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Distribución binomial | Ejercicio resuelto 2: representación mediante tabla y gráfica
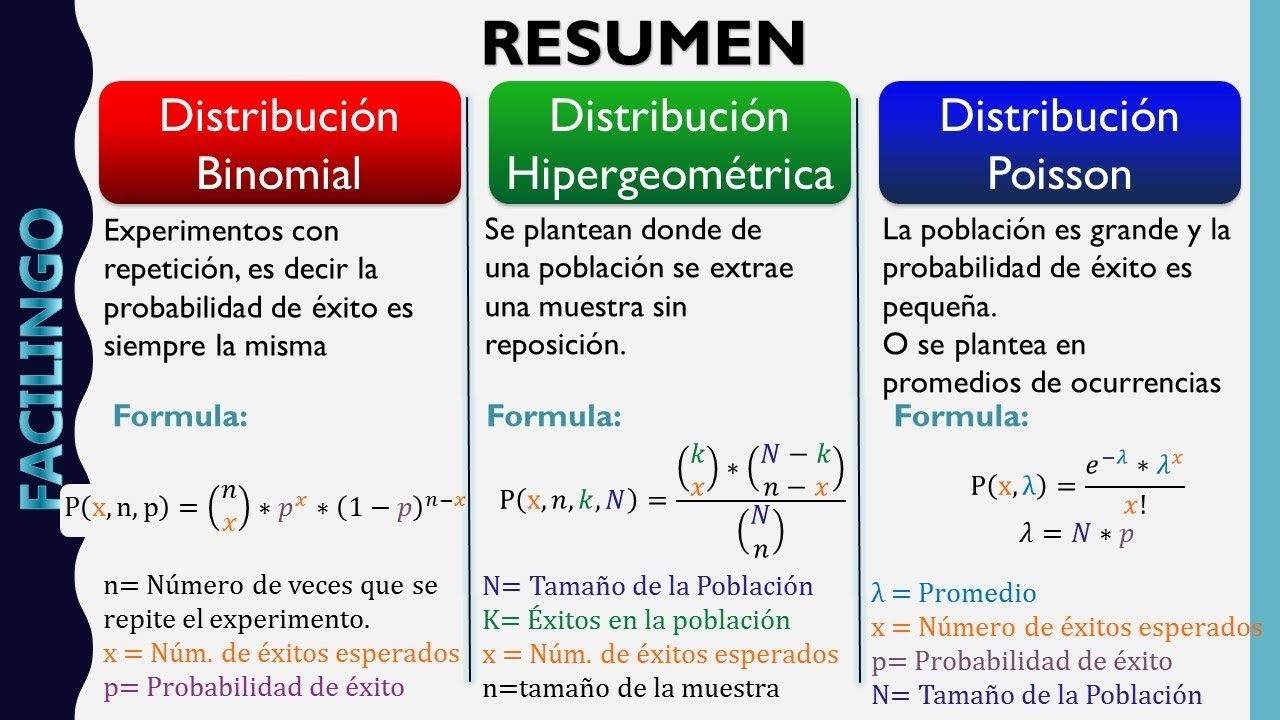
Distribuciones Discretas (Binomial, Hipergeometrica, Poisson)

02 Distribución binomial. Función de probabilidad

Distribución binomial | Ejercicios resueltos | Introducción

18 Momentos estadísticos

Función de probabilidad de variable aleatoria discreta | Ejercicio 1

15 Variable aleatoria y función de distribución acumulativa
5.0 / 5 (0 votes)