FUNCIONES EXPONENCIALES
Summary
TLDREn este video, se explican las funciones exponenciales y las ecuaciones exponenciales, detallando cómo están definidas y cómo se resuelven. Se hace hincapié en que las funciones exponenciales tienen una base positiva distinta de 0 y 1, con una variable independiente en el exponente. Además, se discuten las gráficas de estas funciones, su dominio y las variaciones dependiendo de la base. También se abordan ejemplos y métodos para resolver ecuaciones exponenciales, como igualar bases y exponer la incógnita. Finalmente, se proponen ejercicios prácticos para reforzar los conceptos aprendidos.
Please replace the link and try again.
Q & A
¿Qué características debe tener la base de una función exponencial?
-La base de una función exponencial debe ser un número positivo distinto de 0 y 1. No puede ser un número negativo ni igual a 0 o 1.
¿Cómo se diferencia una función exponencial de una función potencial?
-En una función exponencial, la base es un número constante y la variable está en el exponente, mientras que en una función potencial, la base es la variable y el exponente es un número constante.
¿Cuáles son las dos formas posibles de la gráfica de una función exponencial?
-Las dos formas posibles son: una gráfica que sube (cuando la base es mayor que 1) y una gráfica que baja (cuando la base está entre 0 y 1).
¿Cuál es el dominio de las funciones exponenciales?
-El dominio de las funciones exponenciales es todos los números reales, ya que la función está definida para cualquier valor de x.
¿En qué punto siempre cruzan las gráficas de las funciones exponenciales?
-Las gráficas de las funciones exponenciales siempre cruzan el eje y en el valor 1, independientemente de si la gráfica sube o baja.
¿Cómo se resuelve una ecuación exponencial en la que las bases son diferentes?
-Para resolver una ecuación exponencial con bases diferentes, se debe intentar expresar las bases en términos de la misma base. Una vez que las bases son iguales, se igualan los exponentes.
¿Cómo resolver la ecuación exponencial 2^x = 8?
-Para resolverla, se expresa 8 como 2^3, lo que da 2^x = 2^3. Luego, igualamos los exponentes, es decir, x = 3.
¿Qué hacer si no es posible expresar las bases en términos de la misma base?
-Si no se pueden expresar las bases en la misma base, se debe recurrir a los logaritmos para resolver la ecuación exponencial.
¿Cómo resolver la ecuación 2^(x-5) = 32?
-Primero, se expresa 32 como 2^5, lo que da 2^(x-5) = 2^5. Luego, se igualan los exponentes: x - 5 = 5, y resolviendo, x = 10.
¿Qué propiedad importante de los exponentes se debe recordar al resolver ecuaciones exponenciales?
-Es importante recordar que cualquier número elevado a 0 es igual a 1, es decir, a^0 = 1 para cualquier valor de 'a' distinto de 0.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Funciones EXPONENCIALES y LOGARÍTMICAS: Definición y Propiedades de los Logaritmos.

Funciones exponenciales | Graficar Exponenciales | Precálculo

Función Logarítmica - Ejercicios Nivel 1 - Intro

Aplicación de las funciones logarítmicas y exponenciales en la biología
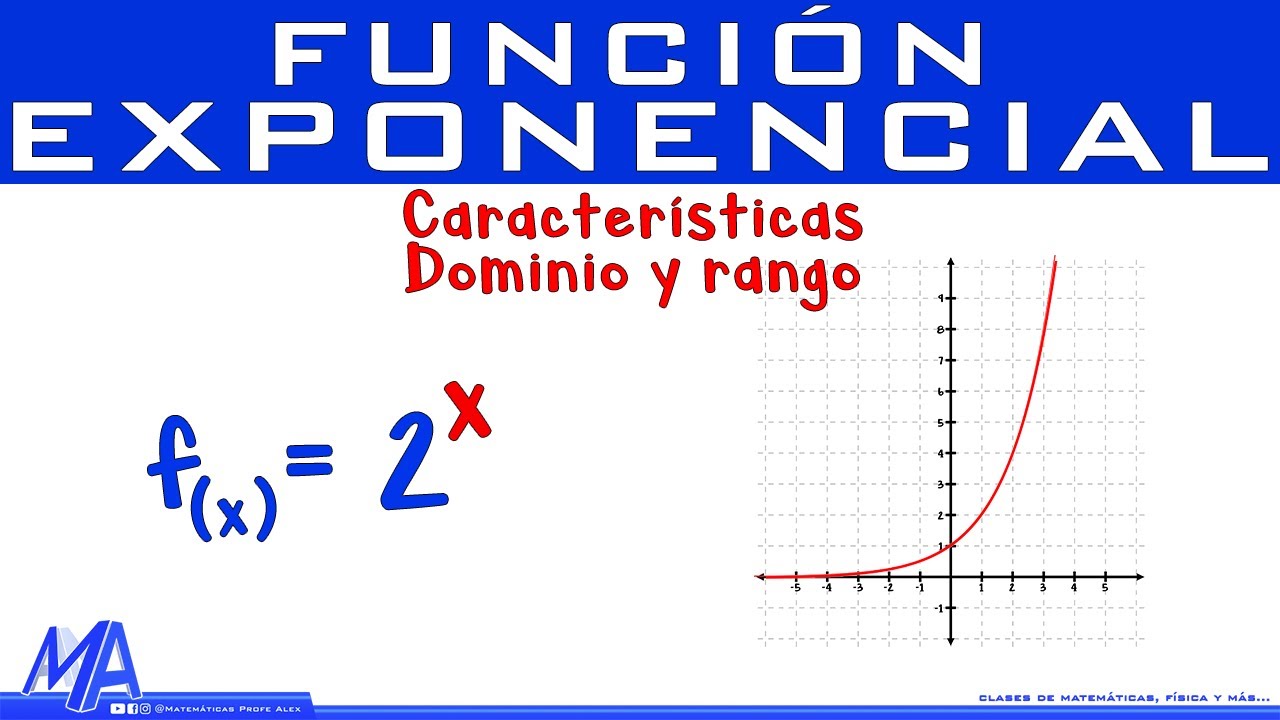
Función Exponencial | Características

Tipos de funciones matemáticas

Aprende la clasificación de las funciones matemáticas en menos de 5 minutos
5.0 / 5 (0 votes)