Volumen entre paraboloide y cilindro con integral doble | POLARES | Ej. 34 Sección 14.3 LARSON
Summary
TLDREn este video, el canal se enfoca en el cálculo del volumen utilizando integrales dobles, específicamente en la sección 14.3 del libro de Larsson. El problema presentado involucra el uso de coordenadas polares para encontrar el volumen de un sólido limitado por gráficos en forma de círculo y parabólica. El host recomienda este ejercicio como un excelente punto de partida para quienes buscan aprender sobre volúmenes en geometría analítica. Se discuten las coordenadas polares y cómo aplicar el cambio de variables para simplificar la integral. Además, se aborda la importancia de la simetría en la resolución del problema y se sugiere el uso de herramientas gráficas para facilitar la comprensión del sólido resultante. Finalmente, se concluye con la resolución de la integral doble y se ofrece recursos adicionales para profundizar en el tema.
Takeaways
- 📚 Se discute sobre el cálculo del volumen utilizando integrales dobles en coordenadas polares, específicamente tomando como referencia el libro de Larsson en su novena edición, sección 14.3.
- 🔢 El problema presentado es de encontrar el volumen de un sólido limitado por gráficos determinados, y aunque puede parecer complicado, es más sencillo de lo que parece.
- 📐 Se recomienda utilizar integrales triples para este tipo de ejercicios, aunque también se pueden usar dobles, ya que ambas técnicas son aplicables y están relacionadas.
- 📈 Se sugiere que este ejercicio sea uno de los primeros a resolver para quienes deseen aprender sobre volumen, ya que es muy básico y ayuda a entender conceptos fundamentales.
- 📈📈 Se destaca la importancia de la integración doble para calcular el volumen, utilizando la región R y la función f(x), teniendo en cuenta el eje x y los límites de integración.
- 📐📏 Se describe cómo cambiar a coordenadas polares, lo cual es esencial para resolver el problema presentado, y cómo la función z se relaciona con el radio en polares.
- 📊 Se menciona que para el círculo de radio 1, la coordenada polar es constante y cómo esto simplifica el cálculo de la integral.
- 📈📊 Se habla sobre el ángulo en las coordenadas polares y cómo este se relaciona con la integración, destacando que el ángulo completo es de 0 a 2pi pero para el problema se considera solo una parte.
- 📐📏 Se detalla el proceso de integración en polares, incluyendo el cambio de variables y cómo se aplican los límites para la integración en el ángulo y el radio.
- 📚📈 Se recomienda el uso de aplicaciones gráficas para visualizar mejor las figuras y las intersecciones, lo que facilita la comprensión del problema y su resolución.
- 📝 Se ofrece recursos adicionales, como secciones de integradores y ejercicios de integrales triples, para quienes deseen profundizar en el tema.
- 📦📏 Se concluye con la resolución del ejercicio, obteniendo un volumen de 7pi/4 unidades cúbicas, y se destaca la belleza matemática de la integración doble en polares.
Q & A
¿De qué trata el video que se está transcribiendo?
-El video trata sobre el cálculo del volumen de un sólido utilizando integrales dobles en coordenadas polares, específicamente siguiendo el enfoque del libro de Larsson para la novena edición, sección 14.3.
¿Qué tipo de figura geométrica se utiliza para encontrar el volumen en este ejercicio?
-Se utiliza un círculo de radio 1, que actúa como una base para el sólido que se está calculando.
¿Por qué es importante recordar la sección de integradores triple que el autor menciona?
-La sección de integradores triple es importante porque proporciona herramientas y ejercicios útiles para aquellos que están aprendiendo sobre integrales triple y temas relacionados, lo que puede ser beneficioso para comprender mejor el tema actual.
¿Qué es una de las recomendaciones que hace el autor para alguien que quiera aprender sobre volumen con integrales?
-El autor recomienda que este ejercicio sea uno de los primeros a resolver si alguien quiere aprender sobre volumen con integrales, ya que es muy básico y puede servir como un buen punto de partida.
¿Qué tipo de cambio de coordenadas se realiza para simplificar el cálculo del volumen?
-Se realiza un cambio de coordenadas cartesianas a polares para simplificar el cálculo del volumen del sólido.
¿Cómo se describe el ángulo en las coordenadas polares en este contexto?
-El ángulo en las coordenadas polares comienza en cero, varía en el semieje x positivo de manera antihoraria y cubre un rango de 0 a 2π.
¿Qué es la ventaja de utilizar coordenadas polares para este ejercicio?
-La ventaja de utilizar coordenadas polares es que simplifica la expresión del volumen del sólido, ya que el radio del círculo es constante y facilita la integración.
¿Qué herramienta o método se sugiere para graficar las funciones y entender mejor el sólido?
-Se sugiere el uso de aplicaciones gratuitas para graficar las funciones, lo que proporciona una mejor comprensión visual del sólido y ayuda en el cálculo.
¿Cómo se describe la intersección del paraboloide con el cilindro en el sólido?
-La intersección del paraboloide con el cilindro se describe como circulares, y estas intersecciones forman las paredes del sólido que está siendo calculado.
¿Cuál es el resultado final del volumen del sólido que se calcula en el video?
-El volumen final del sólido calculado es de 7π/4 unidades cúbicas.
¿Por qué es útil dividir el sólido en partes simétricas para calcular su volumen?
-Dividir el sólido en partes simétricas es útil porque permite simplificar el cálculo, ya que se puede calcular el volumen de una porción y luego multiplicarlo por el número de porciones equivalentes para obtener el volumen total.
¿Cómo se puede verificar la integral doble utilizada en el cálculo del volumen?
-Se puede verificar la integral doble utilizando herramientas de software matemático como Maple, que permite calcular integrales y verificar resultados.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Volumen de z= xy con integral doble | COORDENADAS POLARES | Ej. 33 Sección 14.3 LARSON | GEOGEBRA

Volumen entre 2 cilindros verticales y logaritmo natural | POLARES | Ej. 36 Sección 14.3 LARSON

Volumen de la Bóveda de Viviani en COORDENADAS POLARES | Ej. 37 Sección 14.3 LARSON | GEOGEBRA

Matemáticas. La integral doble

Cálculo de área entre una parábola y 2 rectas con INTEGRALES DOBLES | GEOGEBRA y MAPLE
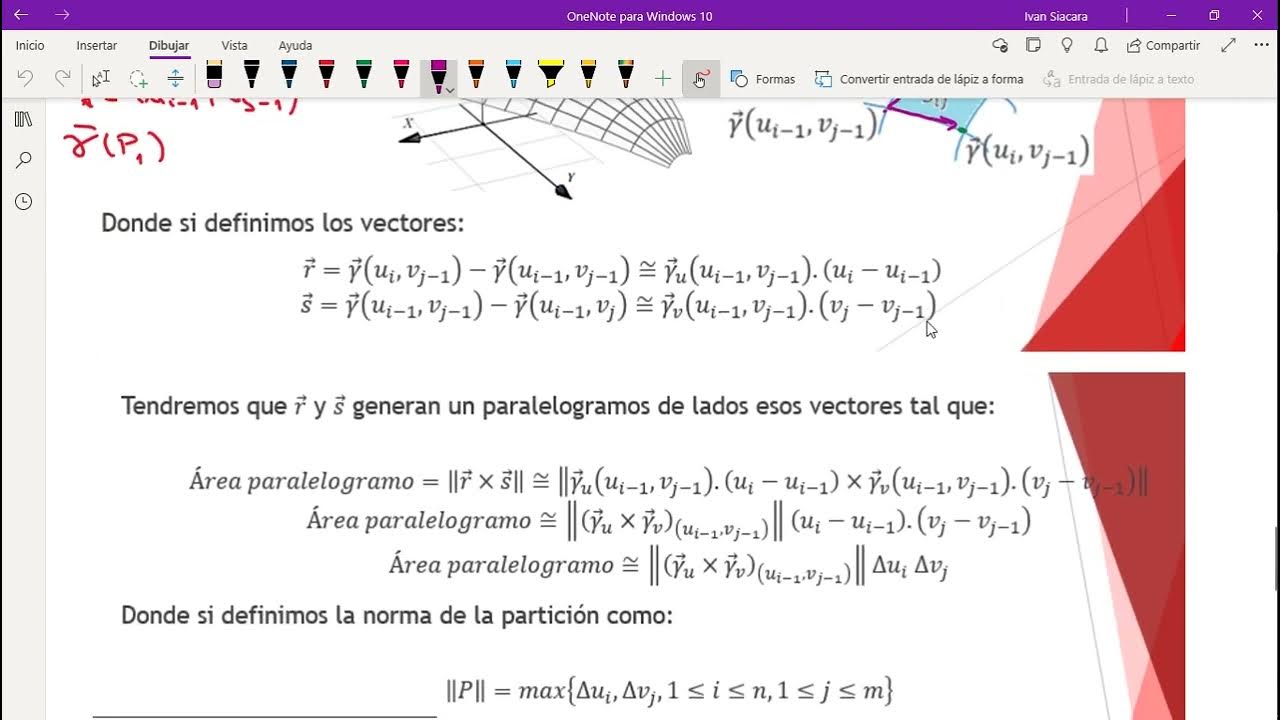
Clase 16 (2da Parte): Integrales de Superficie (campos escalares)
5.0 / 5 (0 votes)