La recta Tangente | Cálculo Diferencial
Summary
TLDREn este video, se explica de manera detallada cómo calcular la recta tangente a una curva utilizando cálculo diferencial. Se abordan dos ejemplos: el primero sobre la parábola y el segundo sobre una hipérbola. El proceso incluye cómo determinar la pendiente de la recta tangente mediante el cálculo del límite y la aplicación de fórmulas estándar de geometría analítica. A lo largo de los ejemplos, se demuestran los pasos para encontrar la ecuación de la recta tangente en un punto específico de la curva, mostrando las aplicaciones prácticas de este concepto en matemáticas y física.
Takeaways
- 😀 La recta tangente es una línea recta que toca una curva en un solo punto, sin cruzarla.
- 😀 El objetivo de calcular la recta tangente es encontrar la pendiente en un punto específico de la curva.
- 😀 La pendiente de la recta tangente se calcula usando el límite de la diferencia entre los valores de la función en dos puntos cercanos.
- 😀 Para obtener la pendiente de la tangente, se utiliza la fórmula del límite: m = lim (x -> a) [(f(x) - f(a)) / (x - a)].
- 😀 El concepto de la tangente tiene aplicaciones en física y cálculo diferencial, como el cálculo de velocidades y razones de cambio.
- 😀 En el ejemplo de la parábola y = x² en el punto (1, 1), se calculó que la pendiente de la tangente es m = 2.
- 😀 La ecuación de la recta tangente se obtiene utilizando la fórmula y - y₁ = m(x - x₁), donde m es la pendiente y (x₁, y₁) es el punto de tangencia.
- 😀 En el ejemplo de la parábola, la ecuación de la tangente en el punto (1, 1) resultó ser y = 2x - 1.
- 😀 En el segundo ejemplo, para la hipérbola y = 3/x en el punto (3, 1), la pendiente de la tangente se calculó como m = -1/3.
- 😀 La ecuación de la tangente en el caso de la hipérbola fue y = -1/3x + 2.
- 😀 El cálculo de la pendiente de la tangente es crucial para entender la tasa de cambio instantánea de una función en un punto específico.
Please replace the link and try again.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Concepto de la derivada explicado fácil y sencillo

Longitud de la Tangente, Normal, Subtangente y Subnormal Clase 1

Derivadas algebraicas y concepto preliminar de una diferencial - ROMATH
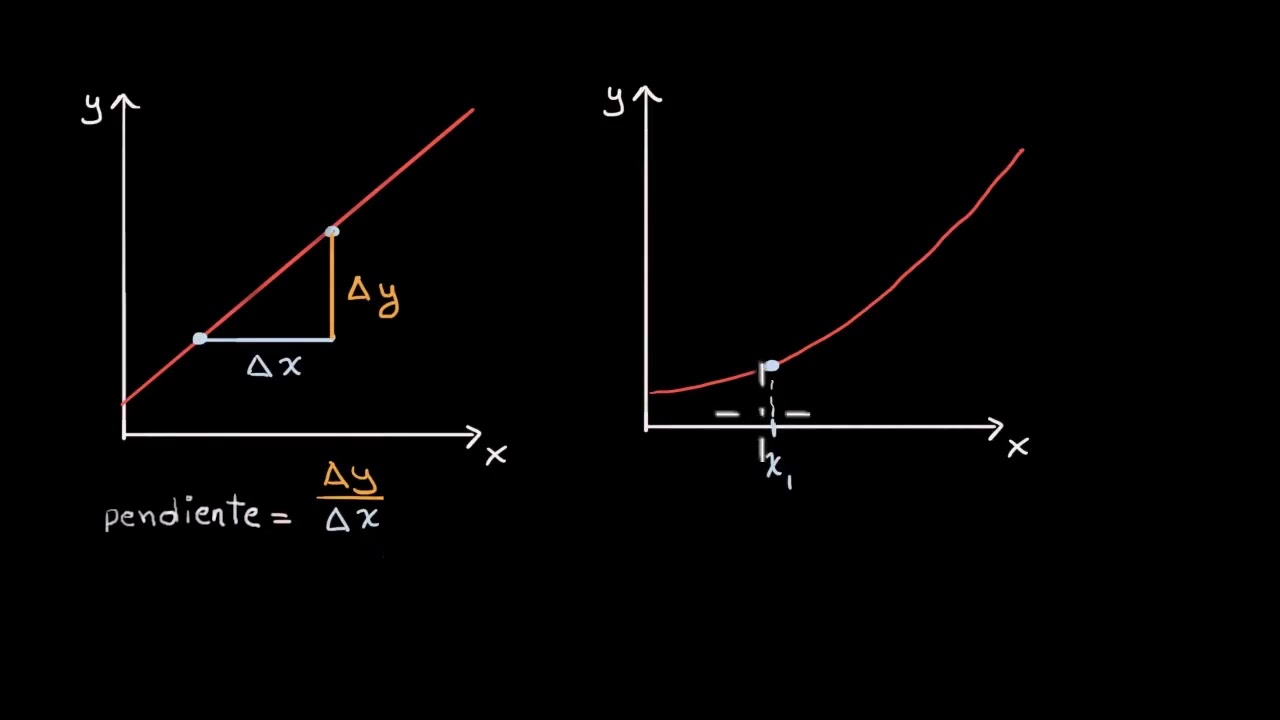
El concepto de derivada | Khan Academy en Español

LA DERIVADA Y LA ECUACIÓN DE LA RECTA TANGENTE

Pendiente de la recta tangente a una curva | Introducción a la derivada

Cálculo de variación: Construcción histórica.
5.0 / 5 (0 votes)