Persamaan Garis Lurus [Part 1] - Mengenal Persamaan Garis Lurus
Summary
TLDRIn this video, Pak Benny introduces the concept of linear equations, focusing on understanding the equation of a straight line (PGL). He explains the general form of the equation y = MX + C, where 'M' represents the gradient and 'C' is the constant. The video covers how to identify linear equations, distinguish them from other types, and plot their graphs on the Cartesian plane. Pak Benny also provides step-by-step instructions for finding the x- and y-intercepts and drawing the graph. Additionally, he tackles examples of equations, clarifies common misconceptions, and demonstrates how to solve problems involving linear equations.
Takeaways
- 😀 Understand the general form of a straight-line equation: y = mx + c, where 'm' is the gradient and 'c' is the y-intercept.
- 😀 The equation of a straight line must have 'x' and 'y' raised to the first power. If they are squared, it is not a straight-line equation.
- 😀 The gradient (m) represents the slope or steepness of the line, and the constant (c) represents the point where the line intersects the y-axis.
- 😀 Example of a straight-line equation: y = 2x + 4, where 2 is the gradient and 4 is the constant.
- 😀 When graphing a straight-line equation, always identify the x-intercept and y-intercept first.
- 😀 The x-intercept is found by setting y = 0 and solving for x, while the y-intercept is found by setting x = 0 and solving for y.
- 😀 A valid straight-line equation will have both x and y to the power of 1, not any higher powers (such as x² or y²).
- 😀 Practice differentiating straight-line equations from non-straight-line equations, such as quadratic or circle equations.
- 😀 A straight-line graph is drawn by plotting the x-intercept and y-intercept, then connecting the two points with a straight line.
- 😀 For a line passing through a specific point, you can check if it satisfies the equation by substituting the coordinates into the equation.
- 😀 The video encourages students to practice graphing lines and solving equations to build a deeper understanding of the material.
Q & A
What is the general form of the equation of a straight line (PGL)?
-The general form of the equation of a straight line is y = MX + C, where M is the gradient (slope) and C is the y-intercept (the point where the line crosses the y-axis).
What do the variables in the equation y = MX + C represent?
-In the equation y = MX + C, 'y' represents the dependent variable, 'x' represents the independent variable, 'M' represents the gradient (or slope) of the line, and 'C' represents the y-intercept, which is the point where the line crosses the y-axis.
How can you identify if a given equation is a linear equation?
-A given equation is a linear equation if both the variables x and y are raised to the power of 1. If either variable has a power other than 1 (e.g., x² or y²), then the equation is not a linear equation.
What is the key distinction between a linear equation and a quadratic equation?
-The key distinction is that in a linear equation, both x and y have an exponent of 1, while in a quadratic equation, one or both of the variables are raised to the power of 2 (e.g., x² or y²).
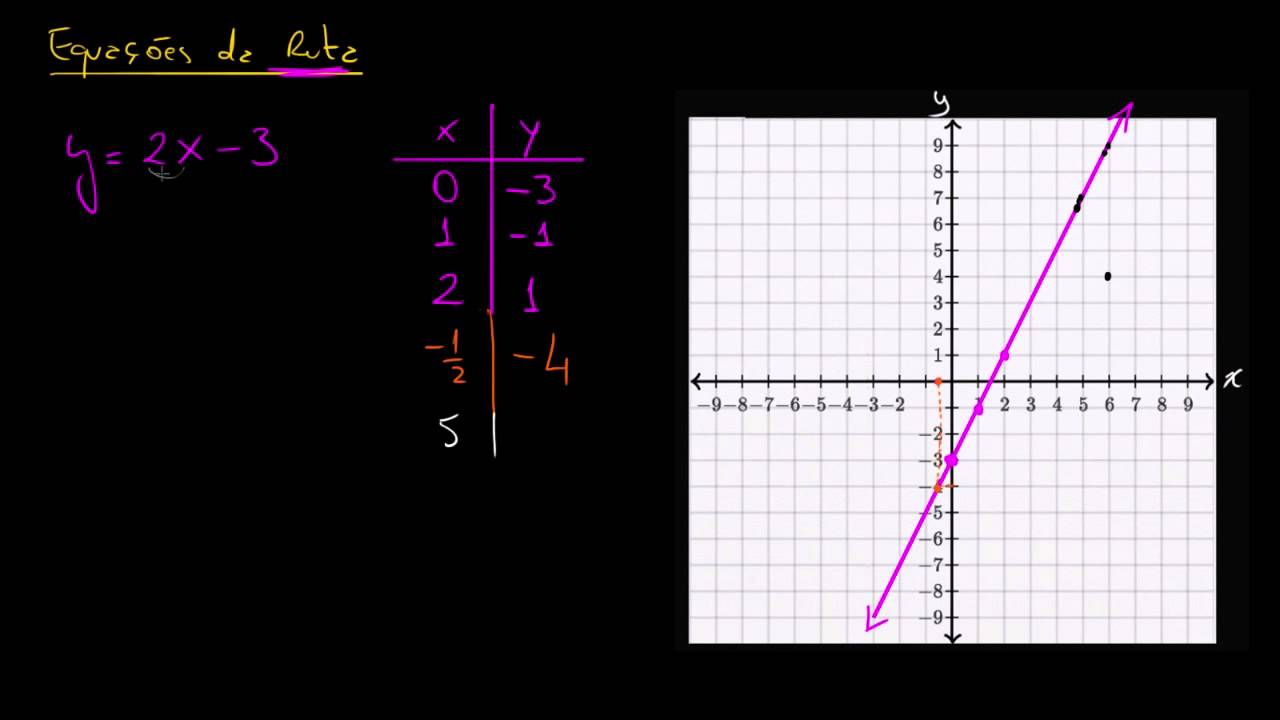
How do you graph the equation of a straight line?
-To graph the equation of a straight line, first find the x-intercept (set y = 0) and the y-intercept (set x = 0). Plot these two points on the coordinate plane, then draw a straight line connecting them.
What is the meaning of the x-intercept and y-intercept in the context of graphing a straight line?
-The x-intercept is the point where the line crosses the x-axis, and the y-intercept is the point where the line crosses the y-axis. To find these intercepts, you set y = 0 for the x-intercept and x = 0 for the y-intercept.
How do you find the x-intercept of the equation y = 2x + 4?
-To find the x-intercept of y = 2x + 4, set y = 0 and solve for x: 0 = 2x + 4, which simplifies to x = -2. Therefore, the x-intercept is (-2, 0).
What is the process to determine the y-intercept of the equation y = 2x + 4?
-To determine the y-intercept of y = 2x + 4, set x = 0 and solve for y: y = 2(0) + 4, which simplifies to y = 4. Therefore, the y-intercept is (0, 4).
What does the gradient (M) of a line tell us about the line's slope?
-The gradient (M) of a line indicates the slope of the line, which tells us how steep the line is. A positive gradient means the line rises from left to right, while a negative gradient means the line falls from left to right.
How do you check if a point lies on a given line in a linear equation?
-To check if a point lies on a given line, substitute the x and y coordinates of the point into the equation. If both sides of the equation are equal, the point lies on the line. If not, the point does not lie on the line.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Persamaan Garis Lurus [Part 3] - Menyusun Persamaan Garis Lurus
Equações lineares com duas variáveis e seus gráficos

Grafik Garis Lurus Hal 207-219 Bab 5 Persamaan Garis Lurus Kelas 8 Kurikulum Merdeka Belajar

Persamaan Linear [Part 1] - Persamaan dan Pertidaksamaan

Ternyata Begini Cara Mencari Gradien Persamaan Garis - Matematika SMP - Persamaan Garis Part 1

Kurikulum Merdeka Matematika Kelas 8 Bab 5 Persamaan Garis Lurus
5.0 / 5 (0 votes)
