INTRODUCCIÓN A LA PROBABILIDAD
Summary
TLDREn este video, se introduce el concepto de probabilidad aplicada en la toma de decisiones cotidianas, como elegir entre diferentes modelos de coches. A través de un ejemplo práctico sobre la duración de los frenos de los autos, se explica cómo la probabilidad se basa en porcentajes de confiabilidad y no en certezas absolutas. Además, se muestra cómo calcular probabilidades utilizando la fórmula básica, explorando situaciones cotidianas como lanzar un dado o resolver problemas más complejos relacionados con eventos aleatorios, como la probabilidad de obtener lámparas defectuosas en una compra.
Takeaways
- 😀 La probabilidad es una rama de las matemáticas que nos ayuda a entender la posibilidad de que ocurra un evento, pero no garantiza su certeza.
- 😀 Al tomar decisiones cotidianas, como la compra de un coche, la probabilidad puede ayudar a evaluar las características y riesgos de cada opción.
- 😀 La probabilidad se calcula usando la fórmula básica: P = n / s, donde 'n' son los resultados favorables y 's' los resultados posibles.
- 😀 En el cálculo de la probabilidad, el evento deseado ('n') es clave, pero también es importante conocer el espacio muestral total ('s').
- 😀 Un ejemplo sencillo de probabilidad es lanzar un dado y calcular la probabilidad de que salga un número específico (por ejemplo, un 2 o un 3).
- 😀 El concepto de espacio muestral es fundamental. En un dado de seis caras, el espacio muestral es 6, ya que hay 6 posibles resultados.
- 😀 Cuando se lanzan dos dados, los problemas de probabilidad se vuelven más complejos, ya que hay que contar todas las combinaciones posibles.
- 😀 La probabilidad no solo se usa para eventos simples. También es útil en situaciones más complejas, como calcular el riesgo de productos defectuosos en una fábrica.
- 😀 En la probabilidad de lámparas defectuosas, la fórmula debe combinar la producción y los defectos de diferentes tipos de lámparas para encontrar una solución.
- 😀 Es esencial comprender las técnicas de conteo y la teoría de conjuntos para resolver problemas de probabilidad más complejos, especialmente en situaciones del mundo real.
Please replace the link and try again.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
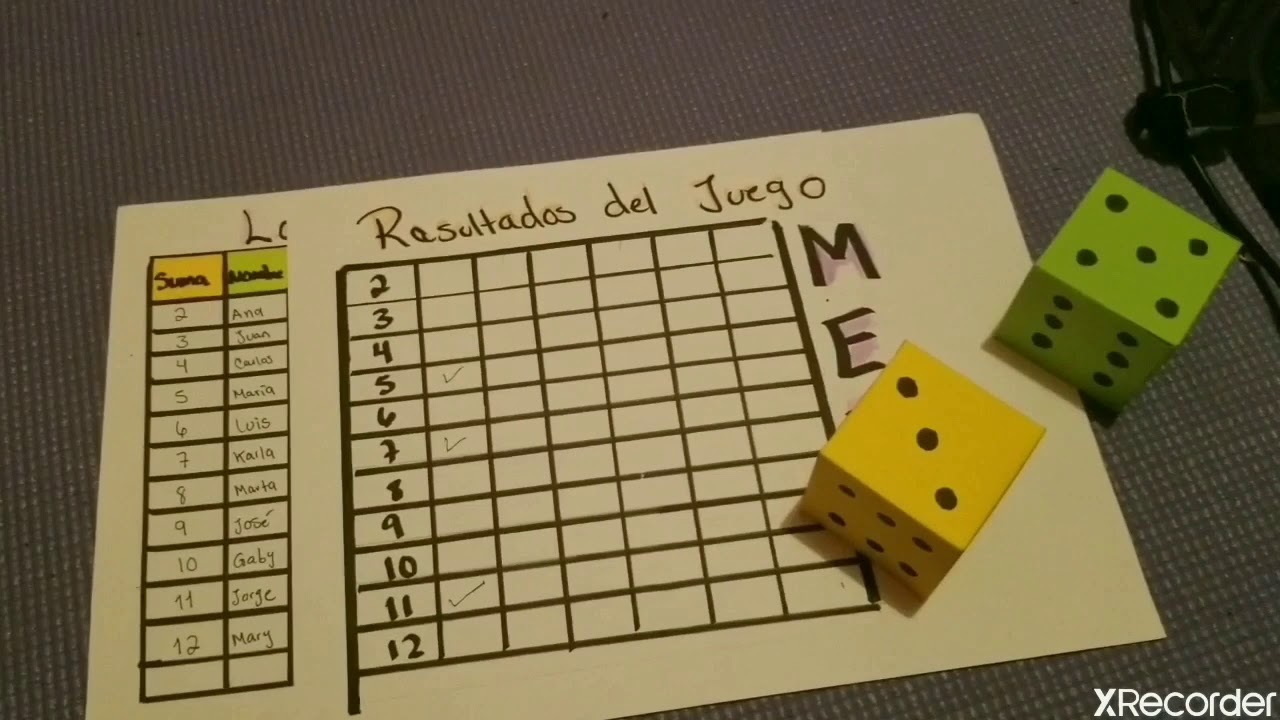
Juego de probabilidad

Progresión 2 PENSAMIENTO MATEMÁTICO I

Riesgo y rendimiento

Toma de decisiones en las Organizaciones ¿Qué es decidir? Analizar vs Ejecutar. Intro - parte 1 de 4

Técnicas de Conteo

Why is Decision Making Important (and How Can You Make Better Choices)?

Problemas didáctico-curriculares de la Educación - Clase 11 - Prof. Mercedes Romero
5.0 / 5 (0 votes)