La probabilidad y sus reglas.
Summary
TLDREn este video se explora el concepto de probabilidad y sus reglas fundamentales, como la regla de multiplicación, la de suma y la de suma-multiplicación. Se explica cómo calcular la probabilidad de eventos independientes y mutuamente excluyentes, usando ejemplos prácticos como lanzar una moneda o encuestas con características como género, uso de lentes y tipo de sangre. El video ofrece una introducción clara y accesible para entender cómo se aplican las probabilidades en situaciones cotidianas y cómo interpretar eventos aleatorios en diferentes contextos.
Takeaways
- 😀 La probabilidad se define como lo que ocurre sobre lo que puede ocurrir, como en el ejemplo de un volado (50% de probabilidad de ganar).
- 😀 La probabilidad de un evento se puede expresar como una fracción, un decimal o un porcentaje (por ejemplo, 0.5 o 50%).
- 😀 Los eventos mutuamente excluyentes no pueden ocurrir simultáneamente, como ser hombre o mujer al mismo tiempo.
- 😀 Los eventos no mutuamente excluyentes pueden ocurrir juntos, como ser mujer, usar lentes y tener un grupo sanguíneo específico.
- 😀 La regla de multiplicación se usa para calcular la probabilidad de eventos independientes concatenados, como ser hombre, usar lentes y tener un grupo sanguíneo específico.
- 😀 La probabilidad de que ocurran eventos independientes se calcula multiplicando las probabilidades de cada evento.
- 😀 La regla de la suma se aplica para eventos mutuamente excluyentes, sumando las probabilidades de eventos que no pueden ocurrir juntos.
- 😀 En eventos mutuamente excluyentes, la probabilidad total será igual a 1 cuando sumes las probabilidades de todos los eventos posibles.
- 😀 La regla de la suma-resta se aplica a eventos no mutuamente excluyentes, donde se suman las probabilidades y se resta la intersección de los eventos.
- 😀 Un ejemplo de la regla de la suma-resta es calcular la probabilidad de que alguien sea mujer o use lentes, restando la probabilidad de que ambas condiciones ocurran simultáneamente.
- 😀 El uso de las probabilidades en contextos prácticos, como encuestas de grupos de personas, puede involucrar tanto eventos mutuamente excluyentes como no mutuamente excluyentes.
Q & A
¿Qué es la probabilidad?
-La probabilidad es la medida de la posibilidad de que ocurra un evento, y se define como la relación entre lo que ocurre y lo que puede ocurrir. Es una forma de cuantificar la incertidumbre de los resultados de un evento.
¿Cómo se calcula la probabilidad de un evento simple, como el lanzamiento de una moneda?
-Para calcular la probabilidad de un evento simple, como el lanzamiento de una moneda, se divide el número de resultados favorables entre el número total de resultados posibles. En este caso, hay dos resultados posibles (cara o cruz), por lo que la probabilidad de ganar en un volado es 0.5 o 50%.
¿Qué significa que los eventos sean mutuamente excluyentes?
-Los eventos mutuamente excluyentes son aquellos que no pueden ocurrir al mismo tiempo. Por ejemplo, en una encuesta, si se pregunta por el género, una persona no puede ser simultáneamente hombre y mujer. Estos eventos no se solapan.
¿Qué es la regla de la multiplicación de probabilidades?
-La regla de la multiplicación se aplica a eventos independientes. Se utiliza cuando se quiere calcular la probabilidad de que ocurran varios eventos de manera secuencial o simultánea. Se obtiene multiplicando las probabilidades de cada evento. Por ejemplo, la probabilidad de que una persona sea varón, use lentes y tenga el grupo sanguíneo 0 es el producto de las probabilidades de cada uno de estos eventos.
¿Qué son los eventos independientes en probabilidad?
-Los eventos independientes son aquellos cuya ocurrencia de uno no afecta la ocurrencia del otro. Por ejemplo, el género de una persona y si usa lentes son eventos independientes, porque el género no influye en si una persona usa lentes o no.
¿Cómo se aplica la regla de la suma en probabilidad?
-La regla de la suma se usa cuando se tienen eventos mutuamente excluyentes, es decir, eventos que no pueden ocurrir al mismo tiempo. La probabilidad de que ocurra uno u otro evento es la suma de las probabilidades individuales. Por ejemplo, la probabilidad de que una persona sea mujer o varón se obtiene sumando las probabilidades de cada evento.
¿Cómo se calculan las probabilidades cuando los eventos no son mutuamente excluyentes?
-Cuando los eventos no son mutuamente excluyentes, se utiliza la regla de la suma multiplicada. En este caso, se suman las probabilidades de los dos eventos, pero se resta la probabilidad de que ambos ocurran al mismo tiempo (la intersección de ambos eventos), para evitar el conteo doble.
¿Qué significa que los eventos no sean mutuamente excluyentes? ¿Puedes dar un ejemplo?
-Los eventos no mutuamente excluyentes son aquellos que pueden ocurrir simultáneamente. Por ejemplo, si una persona puede ser mujer y usar lentes al mismo tiempo, estos eventos no son mutuamente excluyentes. En estos casos, se debe aplicar la regla de la suma multiplicada.
¿Cómo se calcula la probabilidad de que un evento sea A o B, cuando A y B no son mutuamente excluyentes?
-Cuando los eventos A y B no son mutuamente excluyentes, la probabilidad de que ocurra A o B es igual a la suma de las probabilidades de A y B, menos la probabilidad de que ambos ocurran a la vez. La fórmula es: P(A o B) = P(A) + P(B) - P(A y B).
Si una persona tiene un 60% de probabilidad de tener el grupo sanguíneo O y un 20% de tener el grupo sanguíneo B, ¿cuál es la probabilidad de que una persona tenga grupo sanguíneo O o B?
-La probabilidad de que una persona tenga grupo sanguíneo O o B se calcula sumando las probabilidades individuales de cada grupo sanguíneo y restando la probabilidad de que tenga ambos al mismo tiempo. En este caso, como no se pueden tener dos grupos sanguíneos al mismo tiempo, la probabilidad es simplemente 0.6 + 0.2 = 0.8 o 80%.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Jerarquía de las operaciones | Introducción
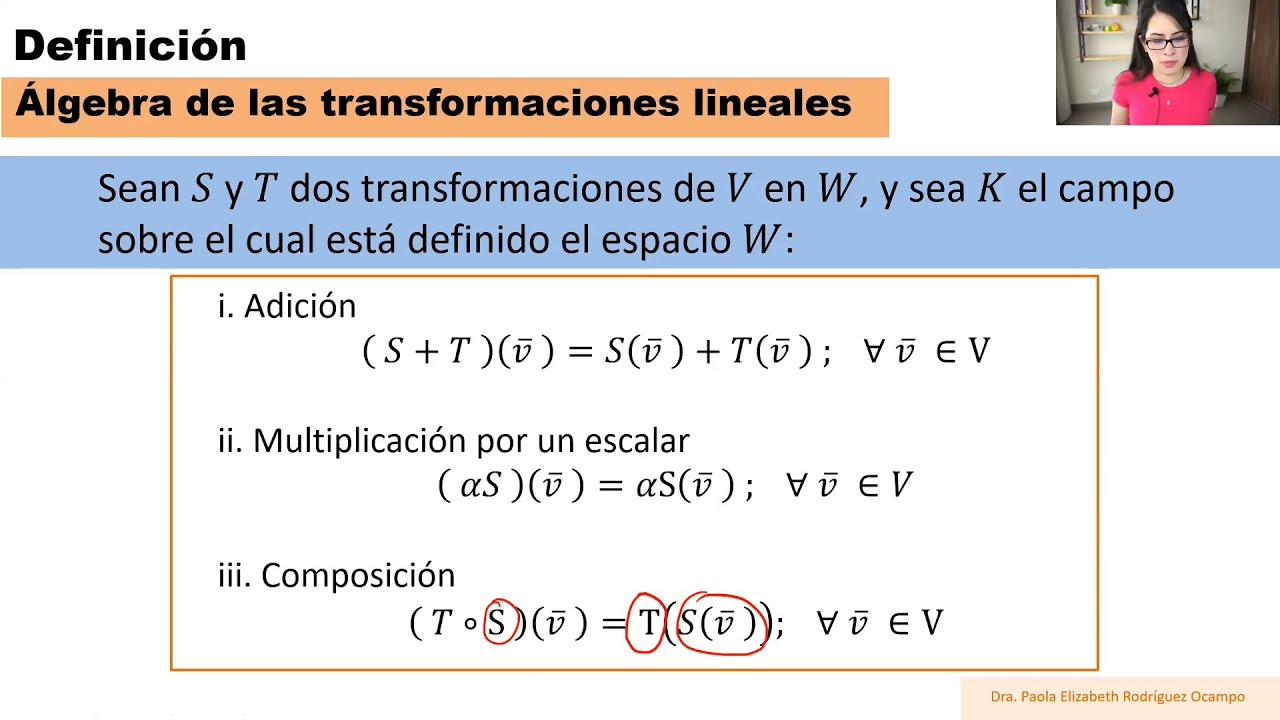
Clase 18 Álgebra Lineal. Transformaciones Lineales - Álgebra de las transformaciones

Tablas de Entrada y Salida | Multiplicación y Sumas

Matemáticas Fundamental I - Propiedades de los números racionales

CURSO SUPER BÁSICO DE PROBABILIDAD, desde cero. Introducción. Lo más importante

Reglas Básicas de las Derivadas
5.0 / 5 (0 votes)
