ILLUSTRATING CIRCULAR FUNCTIONS || PRE-CALCULUS
Summary
TLDRThis instructional video explores circular functions and their relationships through the Pythagorean theorem. It defines key trigonometric functions—sine, cosine, tangent, cosecant, secant, and cotangent—illustrating their calculations based on the coordinates of a point on the unit circle. The video emphasizes the quadrant properties that determine the positivity of these functions. Practical examples clarify how to derive remaining circular functions from given values, enhancing understanding of trigonometric concepts and their applications. Viewers are encouraged to engage with the material for a comprehensive grasp of circular functions.
Takeaways
- 😀 The distance from the origin to point P is represented by the radius r.
- 😀 The horizontal distance from the y-axis is denoted as x, while the vertical distance from the x-axis is y.
- 😀 The Pythagorean theorem is used to establish the relationship: r = √(x² + y²).
- 😀 Six primary circular functions are defined: sine, cosine, tangent, cosecant, secant, and cotangent.
- 😀 Sine is calculated as y/r, cosine as x/r, and tangent as y/x.
- 😀 Cosecant is the reciprocal of sine (r/y), secant is the reciprocal of cosine (r/x), and cotangent is the reciprocal of tangent (x/y).
- 😀 In the unit circle, where r = 1, sine and cosine simplify to y and x, respectively.
- 😀 Quadrant sign rules determine which circular functions are positive in each quadrant.
- 😀 Special angles (30°, 45°, 60°, and 90°) are key for evaluating sine, cosine, and tangent values.
- 😀 Example calculations illustrate how to find remaining circular functions using known values.
Q & A
What is the relationship between the radius (r) and the coordinates (x, y) of a point on a circle?
-The radius r can be calculated using the Pythagorean theorem, where r = √(x² + y²).
How is the sine function defined in the context of a right triangle?
-The sine function, sin(θ), is defined as the ratio of the length of the opposite side (y) to the hypotenuse (r), so sin(θ) = y/r.
What does the cosine function represent?
-The cosine function, cos(θ), is the ratio of the length of the adjacent side (x) to the hypotenuse (r), expressed as cos(θ) = x/r.
How is the tangent function derived from the sine and cosine functions?
-The tangent function, tan(θ), is defined as the ratio of the sine function to the cosine function, or tan(θ) = sin(θ)/cos(θ), which simplifies to tan(θ) = y/x.
What are the reciprocal functions of sine and cosine?
-The reciprocal of sine is cosecant (csc), defined as csc(θ) = r/y, and the reciprocal of cosine is secant (sec), defined as sec(θ) = r/x.
In which quadrants are the circular functions positive?
-In the first quadrant, all circular functions are positive. In the second quadrant, only sine and cosecant are positive. In the third quadrant, tangent and cotangent are positive, and in the fourth quadrant, cosine and secant are positive.
How do you find the remaining circular functions if given one function in a specific quadrant?
-You can use the known function and the Pythagorean identities to derive the other functions based on the signs dictated by the quadrant.
What is the significance of the unit circle in circular functions?
-In the unit circle, the radius r is equal to 1, simplifying the circular functions to sine(θ) = y and cosine(θ) = x.
How do you calculate the radius (r) given coordinates (x, y)?
-Use the formula r = √(x² + y²) to calculate the radius from the given coordinates.
What is the relationship between the sine and cosine of an angle in the unit circle?
-In the unit circle, sine(θ) corresponds to the y-coordinate and cosine(θ) corresponds to the x-coordinate of a point on the circle.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

TRIPEL PYTHAGORAS - TEOREMA PYTHAGORAS (3) - MATEMATIKA SMP KELAS 8
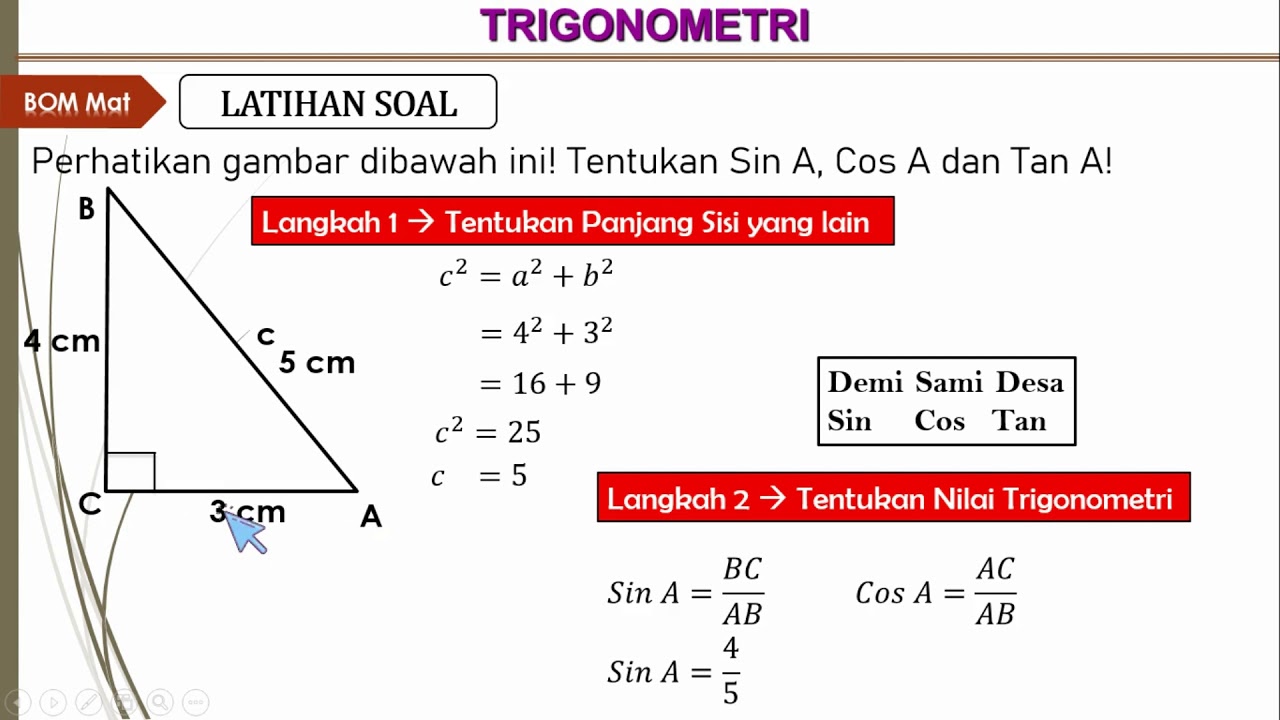
Perbandingan trigonometri pada segitiga siku siku, Menjelaskan rasio trigonometri

10.3 Arcs & Chords

Identitas Trigonometri: Identitas Kebalikan, Perbandingan dan Pythagoras - SMA Kelas 10

Grade 10 Math - Quarter 2 - Lesson 5 - The Relation Among the Chords of a Circle

Soal soal TKA Matematika Jenjang SMP 2026 Materi Geometri dan Pengukuran | Part 3
5.0 / 5 (0 votes)
