8. Método de la Bisección ejercicio parte 1
Summary
TLDREn este video se aborda el método de bisección para encontrar raíces de polinomios. Se inicia identificando un intervalo de confianza y evaluando los extremos para determinar la presencia de una raíz. A través de iteraciones, se calcula una raíz aproximada y se analiza el signo de las evaluaciones para seleccionar el nuevo intervalo. El proceso se repite hasta que el error sea menor al 1%. Se presenta una serie de cálculos detallados que muestran cómo se reduce el error en cada paso, facilitando la comprensión del método y su aplicación en la resolución de ecuaciones.
Takeaways
- 😀 Se presenta el método de la bisección para encontrar raíces de polinomios.
- 😀 Es fundamental identificar un intervalo de confianza donde exista una raíz.
- 😀 Se puede determinar el intervalo de confianza mediante métodos gráficos.
- 😀 Si los signos de la función en los límites del intervalo son opuestos, se garantiza la presencia de una raíz.
- 😀 La fórmula del método de bisección es: x = (a + b) / 2, donde 'a' y 'b' son los límites del intervalo.
- 😀 Se realizan iteraciones sucesivas para aproximar la raíz con mayor precisión.
- 😀 Se calcula el error en cada iteración para evaluar la precisión de la aproximación.
- 😀 El método requiere evaluar la función en los puntos del intervalo y analizar los signos.
- 😀 A medida que se realizan más iteraciones, el error tiende a disminuir.
- 😀 El objetivo es alcanzar un error menor al 1% en las iteraciones finales.
Please replace the link and try again.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Bisección

TEOREMA fundamental del ÁLGEBRA | Comprobando con un EJEMPLO
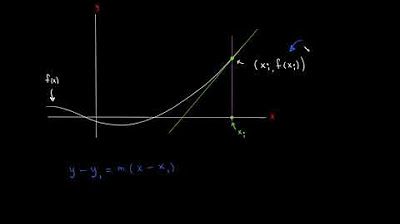
Métodos Numéricos: Newton Raphson

2. Método de Factor Común

PLANEACIÓN DE TRAYECTORIAS (Introducción) | zDynamics

Diferencias entre los métodos abiertos y cerrados

Métodos Numéricos: Método de BISECCIÓN, y colocación e interpretación gráfica.
5.0 / 5 (0 votes)