GRAFICAR FUNCIONES CUADRÁTICAS Super facil
Summary
TLDRDaniel Carreón presenta un tutorial sobre cómo graficar funciones cuadráticas. Explica conceptos básicos del plano cartesiano y cómo identificar coeficientes a, b y c en una ecuación cuadrática. Daniel calcula el vértice de la parábola usando la fórmula x = -b / 2a y luego utiliza valores de x para encontrar los correspondientes valores de y. Finalmente, guía a través del proceso de graficar los puntos en el plano cartesiano, conectándolos para formar una parábola positiva, proporcionando una visión clara del proceso.
Takeaways
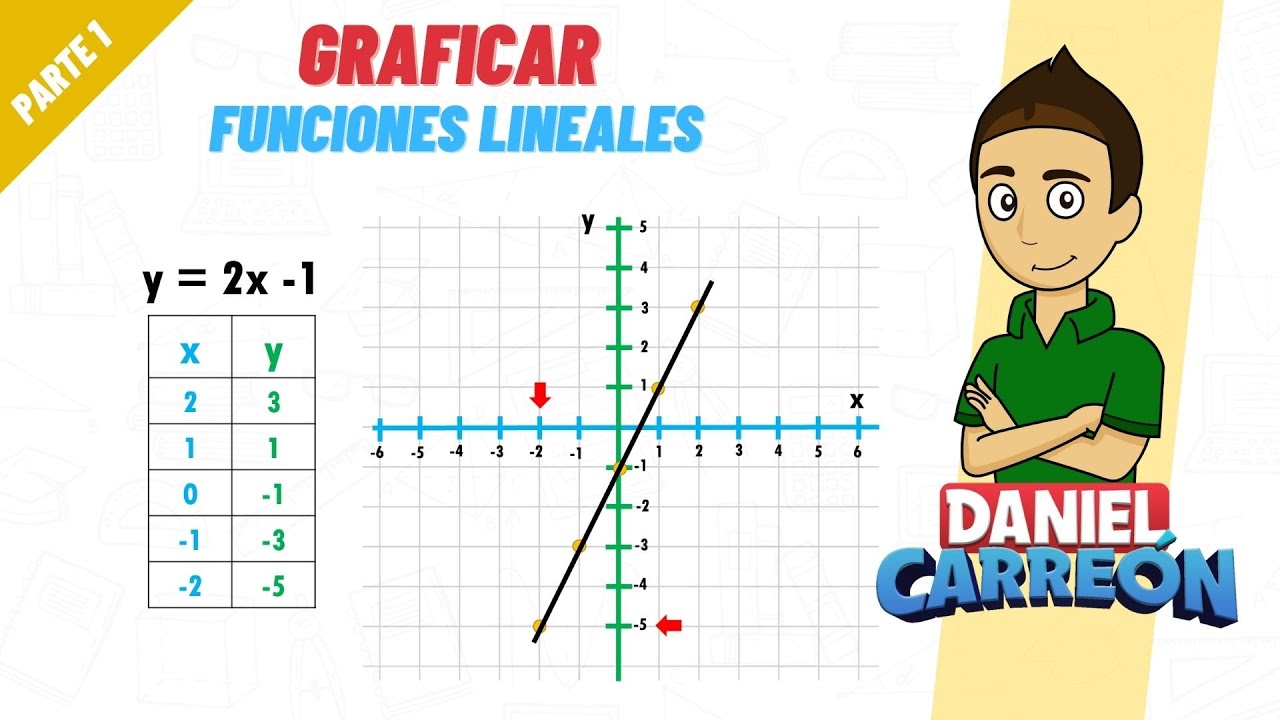
- 📐 El plano cartesiano se compone de dos rectas numéricas: la horizontal (eje de las x) y la vertical (eje de las y), que se intersectan en el origen.
- 📘 Las ecuaciones cuadráticas son aquellas donde la variable x está elevada a la segunda potencia, y su gráfica representa una parábola.
- 📈 La parábola puede ser positiva (abre hacia arriba) o negativa (abre hacia abajo), y su punto extremo se llama vértice.
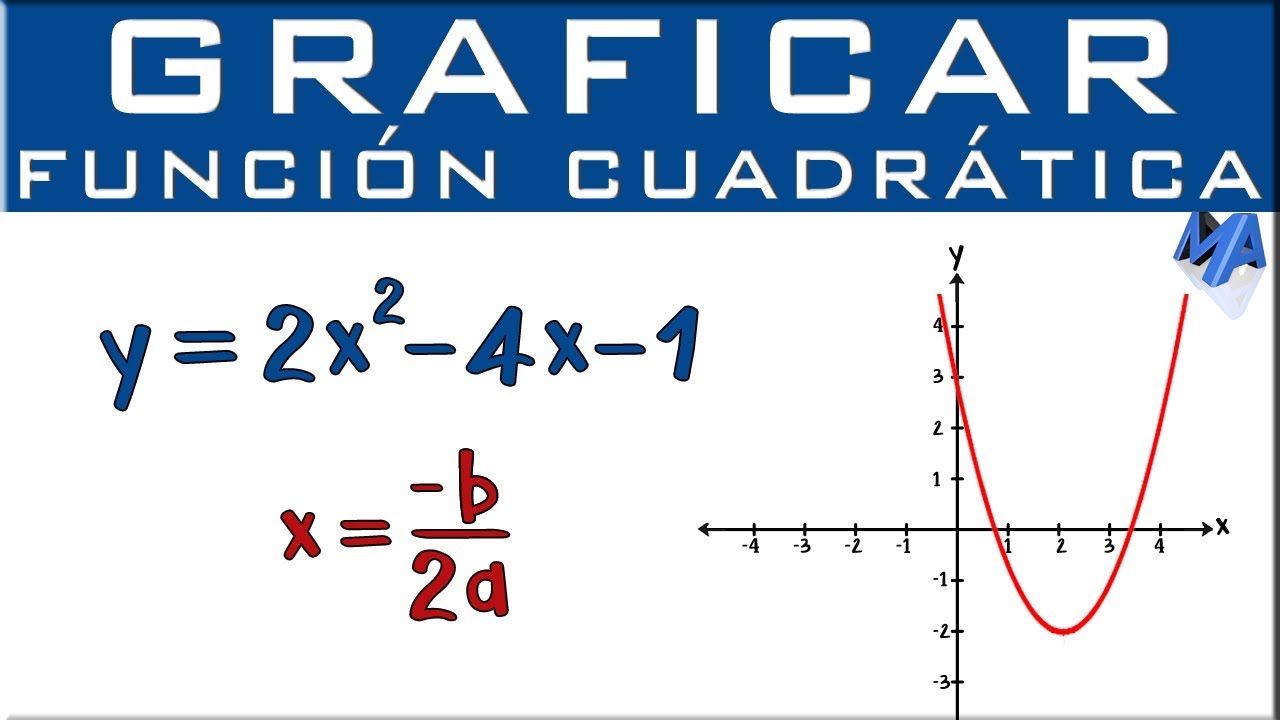
- 🔢 Para encontrar el vértice de una parábola, se utiliza la fórmula x = -b / 2a, donde a y b son coeficientes de la ecuación.
- 📊 Se puede construir una tabla con valores de x y sus correspondientes y para trazar la parábola en el plano cartesiano.
- ✍️ En el ejemplo dado, la ecuación dada es y = x^2 - 6x + 9, y se determina que a = 1, b = -6 y c = 9.
- 🧮 Al aplicar la fórmula del vértice, se encuentra que x = 3, y al sustituir en la ecuación, se obtiene y = 0, por lo que el vértice es (3, 0).
- 📍 Se eligen valores de x antes y después del vértice para calcular los puntos correspondientes a y y trazar la parábola.
- 📈 Al graficar los puntos (1, 4), (2, 1), (3, 0), (4, 1) y (5, 4) en el plano cartesiano, se forma una parábola positiva.
- 🎓 Este vídeo sirve como una guía para entender cómo graficar funciones cuadráticas y cómo encontrar el vértice de una parábola.
Q & A
¿Qué es el plano cartesiano?
-El plano cartesiano consiste en dos rectas numéricas, una horizontal (eje de las x o abscisas) y una vertical (eje de las y u ordenadas), que se cortan en un punto llamado origen.
¿Qué es una ecuación cuadrática?
-Una ecuación cuadrática es una ecuación en la que la variable x está elevada a la segunda potencia, y su gráfica es una parábola.
¿Cómo se identifica si una parábola es positiva o negativa?
-Si la parábola tiene su punto más bajo hacia arriba, se considera positiva. Si tiene su punto más alto hacia abajo, se considera negativa.
¿Qué es el vértice de una parábola?
-El vértice es el punto más bajo o más alto de la parábola, dependiendo de si es positiva o negativa.
¿Cuál es la fórmula para encontrar el vértice de una parábola?
-La fórmula para encontrar el vértice es x = -b / 2a, donde b es el coeficiente de x y a es el coeficiente de x² en la ecuación cuadrática.
En la ecuación y = x² - 6x + 9, ¿cuáles son los valores de a, b y c?
-En la ecuación y = x² - 6x + 9, a = 1, b = -6 y c = 9.
¿Cómo se calcula el valor del vértice de la parábola para la ecuación y = x² - 6x + 9?
-Usando la fórmula x = -b / 2a, se sustituye b = -6 y a = 1, resultando en x = 3. El vértice en x es 3.
¿Qué valores de x se usan para graficar la parábola en el ejemplo del video?
-Se usan los valores de x: 1, 2, 3, 4 y 5 para graficar la parábola.
¿Cuál es el valor de y cuando x = 3 en la ecuación y = x² - 6x + 9?
-Cuando x = 3, el valor de y es 0, por lo tanto el vértice de la parábola está en el punto (3, 0).
¿Cómo se grafican los puntos obtenidos en el plano cartesiano?
-Se ubican los puntos en el plano cartesiano, buscando el valor de x en el eje horizontal y el valor de y en el eje vertical. Los puntos se conectan para formar la parábola.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
5.0 / 5 (0 votes)