Hallar la ecuación general de la CIRCUNFERENCIA conociendo el centro y el radio EJEMPLO 2
Summary
TLDREn este video, se enseña a encontrar la ecuación general de una circunferencia a partir de su centro y radio. A través de un ejemplo práctico, el presentador explica cómo aplicar la fórmula canónica de la circunferencia y el proceso de desarrollo de la ecuación. Se enfatizan conceptos clave como el cuadrado de un binomio y la simplificación de términos. Al final, se obtiene la ecuación general, destacando la importancia de estos cálculos en la geometría. El video invita a los espectadores a explorar más sobre el tema en el canal y a interactuar con el contenido.
Takeaways
- 😀 La ecuación de la circunferencia se basa en conocer el centro (H, K) y el radio (R).
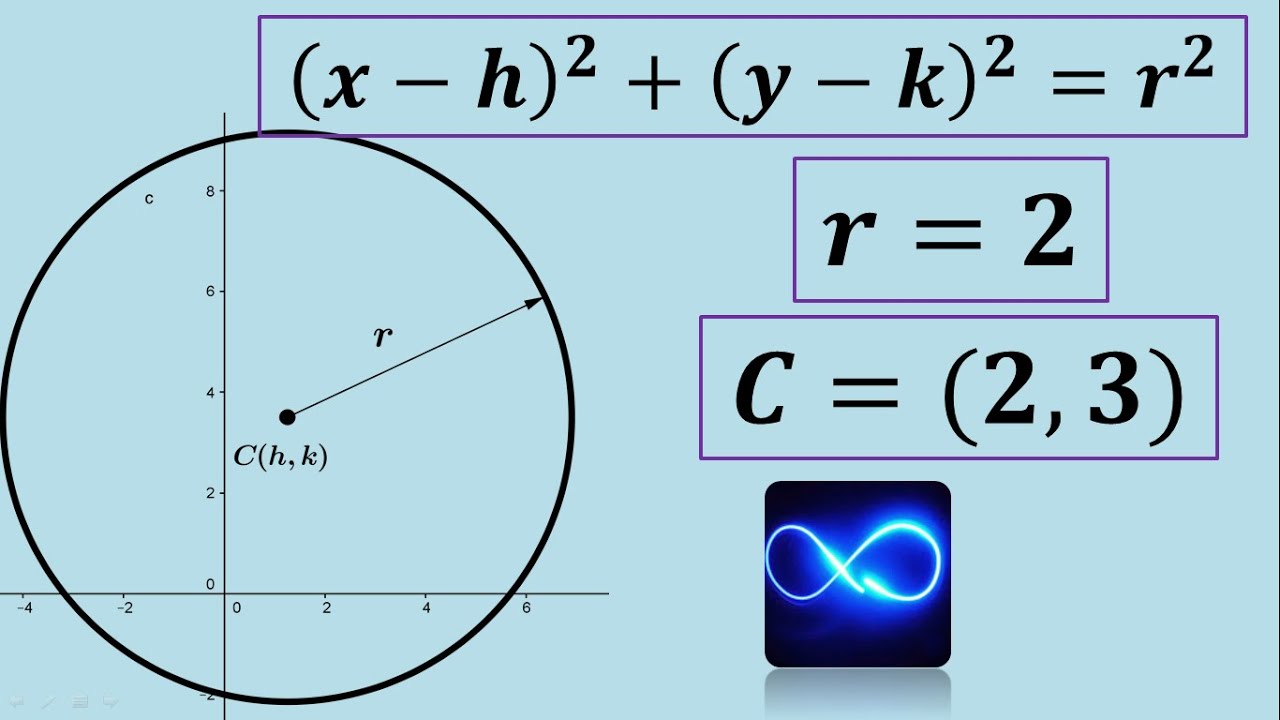
- 😀 La forma canónica de la ecuación de la circunferencia es: (x - h)² + (y - k)² = r².
- 😀 En el ejemplo, el centro de la circunferencia es (-3, 5) y el radio es √20.
- 😀 Para escribir la ecuación canónica, se sustituyen H, K y R en la fórmula.
- 😀 La expansión de (x + 3)² se realiza como x² + 6x + 9.
- 😀 La expansión de (y - 5)² se realiza como y² - 10y + 25.
- 😀 Al combinar los términos, se simplifica la ecuación a x² + y² + 6x - 10y + 34 = 20.
- 😀 Para obtener la ecuación general, se mueve el número del lado derecho al izquierdo.
- 😀 La ecuación general de la circunferencia se expresa como x² + y² + 6x - 10y + 14 = 0.
- 😀 Se invita a los espectadores a suscribirse y participar en el curso completo disponible.
Q & A
¿Cuál es el objetivo del video?
-El objetivo del video es enseñar cómo encontrar la ecuación general de una circunferencia a partir del centro y el radio.
¿Qué información es necesaria para resolver el ejercicio?
-Es necesario conocer las coordenadas del centro (H, K) y el radio (R) de la circunferencia.
¿Cuál es la fórmula canónica de la circunferencia?
-La fórmula canónica de la circunferencia es (x - H)² + (y - K)² = R².
En el ejemplo, ¿cuáles son las coordenadas del centro?
-Las coordenadas del centro son (-3, 5).
¿Qué valor tiene el radio en el ejemplo?
-El valor del radio en el ejemplo es √20.
¿Cómo se sustituyen los valores en la fórmula canónica?
-Se sustituyen los valores de H, K y R en la fórmula canónica, resultando en (x + 3)² + (y - 5)² = 20.
¿Qué pasos se siguen para expandir los binomios?
-Se utiliza la fórmula del cuadrado de un binomio: a² + 2ab + b², considerando los signos correctamente.
¿Cuál es la forma general de la ecuación de la circunferencia al final?
-La forma general de la ecuación de la circunferencia es x² + y² + 6x - 10y + 14 = 0.
¿Qué ocurre con los números al final del proceso?
-Los números se reorganizan y se combinan para obtener la ecuación general, moviendo el término constante al lado izquierdo.
¿Qué invita el instructor a hacer al final del video?
-El instructor invita a los espectadores a suscribirse, comentar, compartir y dar 'like' al video.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Circunferencias: De general a ordinaria | Matemáticas | Khan Academy en Español

Find center and radius of circumference (completing perfect square trinomial)

Encontrar el centro y radio de la CIRCUNFERENCIA conociendo la ecuación general EJEMPLO 2

Ecuación de la circunferencia con centro fuera del origen (tercera parte).
Ordinary and general equation of circumference with given center and radius (Example 1)

Ejercicio 4 de Circunferencia
5.0 / 5 (0 votes)