Transformaciones lineales | Álgebra lineal
Summary
TLDREste video de Mathete se centra en las transformaciones lineales, explicando su definición como funciones que convierten vectores en otros vectores. Se presentan conceptos clave como dominio, codominio y espacios vectoriales. Además, se destacan las condiciones necesarias para que una transformación sea lineal: aditividad y homogeneidad. A través de ejemplos, el video demuestra cómo verificar si una transformación cumple con estas condiciones, proporcionando un entendimiento claro y accesible de este importante concepto en álgebra lineal.
Takeaways
- 😀 Una transformación lineal es una función que toma vectores como entrada y produce vectores como salida.
- 😀 En el contexto de las transformaciones lineales, el dominio y el codominio se denominan espacios vectoriales, V y W respectivamente.
- 😀 La aditividad es una propiedad esencial: T(u + v) debe ser igual a T(u) + T(v) para que una transformación sea lineal.
- 😀 La homogeneidad también es fundamental: T(αv) debe ser igual a αT(v), donde α es un escalar.
- 😀 No todas las transformaciones son lineales; deben cumplir con las condiciones mencionadas para ser clasificadas como tales.
- 😀 La función toma un valor, lo procesa y devuelve un único valor; esto se aplica a vectores en el caso de transformaciones lineales.
- 😀 Se puede transformar un vector de R² (dos componentes) a R³ (tres componentes) y viceversa.
- 😀 En el ejemplo, al sumar dos vectores y luego transformarlos, el resultado debe coincidir con transformar cada vector por separado y luego sumarlos.
- 😀 La verificación de las propiedades se realiza utilizando vectores genéricos en lugar de vectores específicos con valores numéricos.
- 😀 Si se cumplen ambas propiedades (aditividad y homogeneidad), se confirma que la transformación es lineal.
Q & A
¿Qué es una transformación lineal?
-Una transformación lineal es una función que toma un vector como entrada y produce otro vector como salida, a menudo cambiando sus dimensiones.
¿Cuál es la diferencia entre el dominio y el codominio en el contexto de funciones?
-El dominio son los valores que se introducen en la función, mientras que el codominio son los valores que la función devuelve.
¿Qué representan los espacios vectoriales en el contexto de las transformaciones lineales?
-Los espacios vectoriales son conjuntos de vectores que pueden ser transformados, donde el dominio se llama 'v' y el codominio 'w'.
¿Cuáles son las dos condiciones que deben cumplirse para que una transformación sea lineal?
-Las dos condiciones son: la aditividad (T(u + v) = T(u) + T(v)) y la homogeneidad (T(αv) = αT(v)).
¿Qué es la aditividad en las transformaciones lineales?
-La aditividad significa que la transformación de la suma de dos vectores es igual a la suma de sus transformaciones.
¿Cómo se define la homogeneidad en el contexto de transformaciones lineales?
-La homogeneidad establece que la transformación de un vector multiplicado por un escalar es igual al escalar multiplicado por la transformación del vector.
¿Qué ejemplos se utilizan para ilustrar las transformaciones lineales?
-Se utilizan ejemplos de vectores en R² (dos dimensiones) que se transforman en vectores en R³ (tres dimensiones) y viceversa.
¿Por qué es importante verificar si una transformación es lineal?
-Es importante porque no todas las transformaciones son lineales, y verificar la linealidad ayuda a entender el comportamiento de la transformación.
¿Qué tipo de componentes pueden tener los vectores en R² y R³?
-Los vectores en R² tienen dos componentes, mientras que los vectores en R³ tienen tres componentes.
¿Qué debe hacerse para comprobar si una transformación específica es lineal?
-Se deben aplicar las condiciones de aditividad y homogeneidad a la transformación y verificar si se cumplen con vectores genéricos.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Transformaciones lineales Definición y propiedades

Transformaciones lineales y matrices | Esencia del álgebra lineal, capítulo 3

Vectores propios y valores propios | Esencia del álgebra lineal, capítulo 10
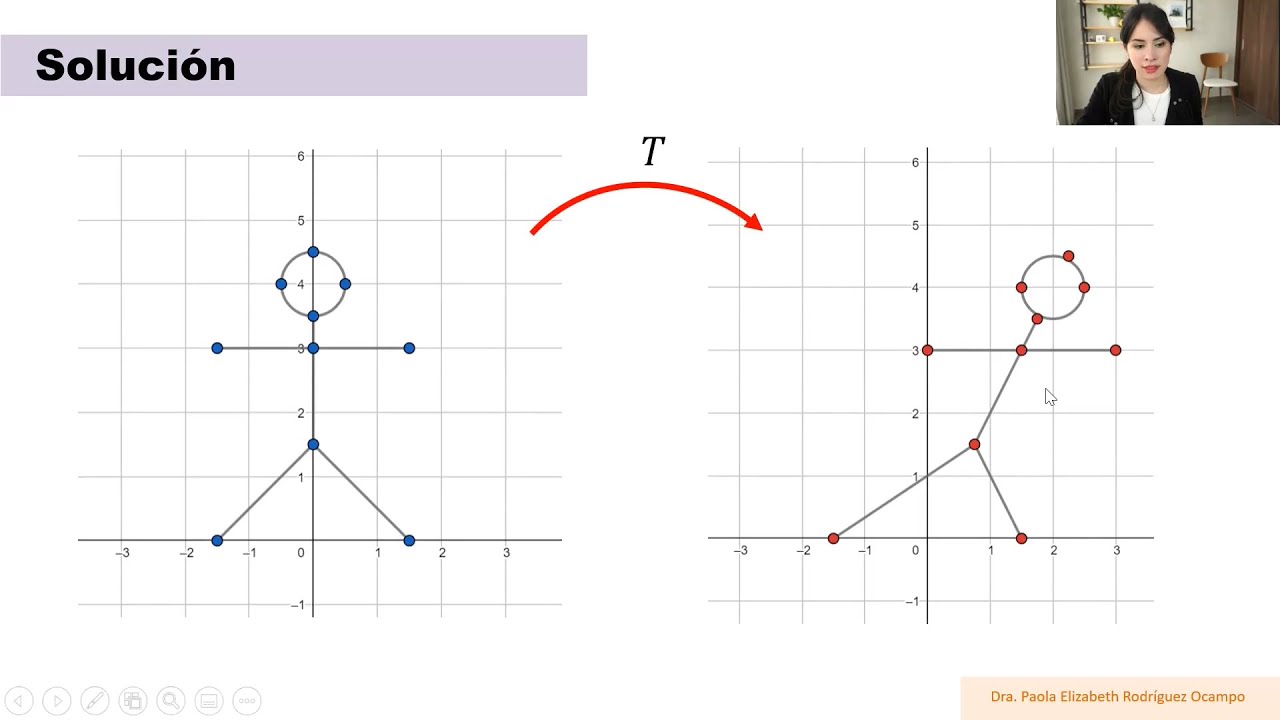
Clase 15 Álgebra Lineal. Transformaciones Lineales - Introducción
Vectores en un espacio abstracto | Esencia del álgebra lineal, capítulo 11

Transformaciones lineales
5.0 / 5 (0 votes)