Learn Big O notation in 6 minutes 📈
Summary
TLDRIn this video, the host introduces Big O notation, a key concept in computer science that describes algorithm performance as data volume increases. He explains various complexities such as O(1), O(n), O(log n), O(n log n), O(n²), and O(n!) with practical examples. The host emphasizes the significance of understanding these notations for algorithm efficiency, illustrating how performance varies with data size. He concludes with a grading system for each complexity, reinforcing that while smaller datasets may yield different results, the overall aim is to grasp the essence of algorithm efficiency.
Takeaways
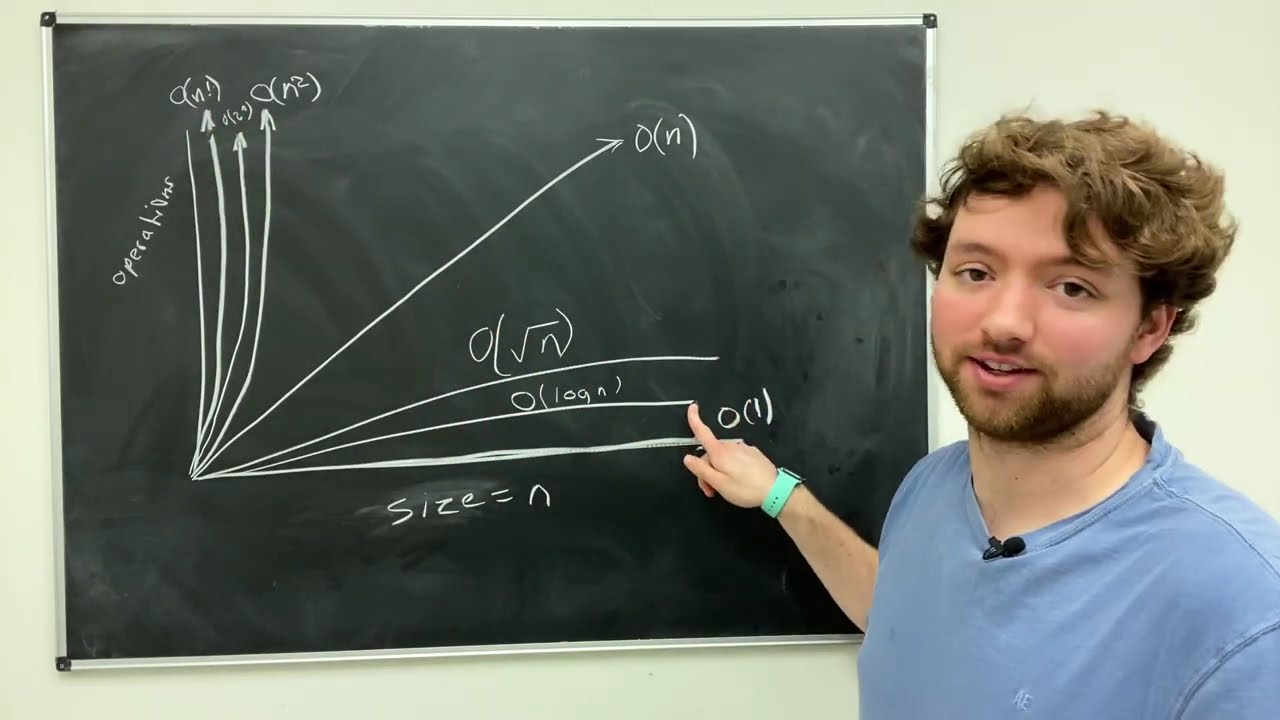
- 😀 Big O notation describes how the performance of an algorithm changes as the amount of data increases.
- 📈 It focuses on the number of steps required to complete an algorithm rather than the speed of execution on different machines.
- 🔍 Smaller operations are often ignored in Big O notation; for example, n + 1 simplifies to n.
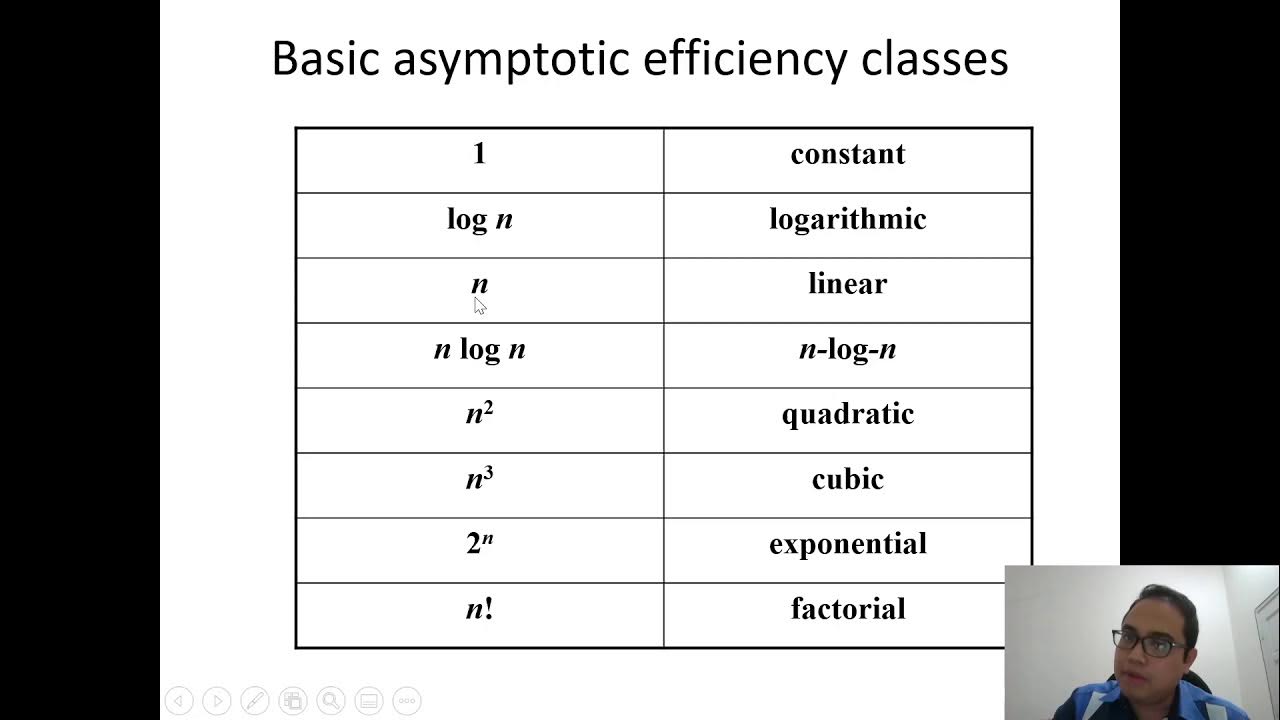
- ⚙️ Common complexities include O(1), O(n), O(log n), O(n^2), and O(n!) where n represents the size of the data.
- 📊 O(1) indicates constant time, meaning performance does not change regardless of data size.
- 🔄 O(log n) represents logarithmic time, such as in binary search, where performance improves as data grows.
- ⬆️ O(n) indicates linear time complexity, meaning the performance scales proportionally with data size.
- 🔄 O(n log n) is quasi-linear time, typical for sorting algorithms like quicksort and mergesort.
- ⚠️ O(n^2) signifies quadratic time, which can become very slow with large datasets, such as with bubble sort.
- 🚫 O(n!) represents factorial time, which is extremely slow, exemplified by problems like the traveling salesman.
Q & A
What is Big O notation?
-Big O notation is a mathematical representation used to describe the performance or complexity of an algorithm in relation to the size of the input data. It focuses on how the runtime or space requirements grow as the amount of data increases.
Why is Big O notation important in computer science?
-Big O notation is important because it allows developers to evaluate the efficiency of algorithms, helping them choose the right algorithm for the task based on expected input size and performance.
What does the term 'O(1)' represent?
-O(1), or constant time, indicates that the execution time of an algorithm does not change regardless of the size of the input data. Examples include accessing an element in an array or inserting at the beginning of a linked list.
Can you explain O(n) and its significance?
-O(n) represents linear time complexity, meaning the execution time grows linearly with the size of the input data. For instance, looping through an array takes time proportional to the number of elements.
What is the difference between O(n) and O(n^2)?
-O(n) indicates linear growth, while O(n^2) indicates quadratic growth. In O(n^2), the time required increases with the square of the input size, making it significantly slower for large datasets compared to linear time.
What does O(log n) signify?
-O(log n) indicates logarithmic time complexity, where the time required decreases significantly as the input size increases. This is common in algorithms like binary search.
How does O(n log n) compare to other complexities?
-O(n log n) is known as quasi-linear time. It is generally more efficient than O(n^2) for large datasets but slower than O(n) and O(log n). Common algorithms with this complexity include quicksort and mergesort.
What does O(n!) represent in terms of performance?
-O(n!) represents factorial time complexity, which grows extremely fast and is considered highly inefficient for large datasets. An example of an algorithm with this complexity is the traveling salesman problem.
How do smaller operations affect Big O notation?
-In Big O notation, smaller operations are often ignored because they have a negligible impact on the overall performance when analyzing the algorithm's efficiency at scale.
What grades were assigned to the different runtime complexities?
-In the video, O(1) received an 'A', O(log n) a 'B', O(n) a 'C', O(n log n) a 'D', O(n^2) an 'F', and O(n!) was noted as being even worse, leading to expulsion from school.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

2 1 The Gist 14 min
Time Complexity and Big O Notation - Data Structures and Algorithms
CSC645 - Chapter 1 (Continued) - Fundamentals of Algorithm Analysis

Time Complexity | Big O Notation | Data Structures & Algorithms | JomaClass

Asymptotic Notation | Big O Notation | Omega Notation | Big Theta Notation | Most Imp. in Algorithm

Complete Beginner's Guide to Big O Notation
5.0 / 5 (0 votes)
