Preorder Traversal in a Binary Tree (With C Code)
Summary
TLDRIn this video, the speaker provides an in-depth explanation of preorder traversal in binary trees. Starting with a basic introduction to tree traversals, the speaker explains how preorder traversal works by visiting the root node first, followed by the left subtree, and then the right subtree. Using a sample tree, the process is demonstrated step by step. Additionally, a recursive function for preorder traversal in C programming is explained. The speaker highlights how recursion simplifies traversal tasks and concludes with a demonstration of the code in action, emphasizing its simplicity.
Takeaways
- 🌳 Preorder traversal is a method for traversing a tree data structure.
- 📝 The mnemonic for remembering the order of traversal is 'Left-Right-Root' for preorder.
- 🔑 The key steps in preorder traversal are: visit the root node first, then the left subtree, and finally the right subtree.
- 👨🏫 The video uses a visual example of a tree to demonstrate how preorder traversal is performed.
- 📑 The script explains a technique to remember the order of traversal by writing 'Root', 'Left', and 'Right' in their respective order.
- 💡 The script emphasizes the importance of understanding the difference between preorder, inorder, and postorder traversals.
- 🛠️ Recursion is used in the code to implement the preorder traversal function, simplifying the process.
- 💻 The script provides a pseudo code example for the preorder traversal function, highlighting the simplicity of the approach.
- 🔍 Preorder traversal can be used for searching or processing all nodes in a tree, as it visits every node.
- 📈 The video script includes a step-by-step guide on how to code the preorder traversal function in a programming language.
Q & A
What is preorder traversal in a binary tree?
-Preorder traversal is a tree traversal method where the root node is visited first, followed by the left subtree and then the right subtree. The sequence is Root, Left, Right.
How can you remember the order of preorder traversal?
-A simple way to remember the order is to write the word 'Root' first, followed by 'Left' and 'Right'. This reminds you that in preorder traversal, you visit the root node first, then the left subtree, and finally the right subtree.
What would the preorder traversal be for the tree given in the script?
-The preorder traversal for the given tree is 4, 1, 5, 2, 6.
What happens if the root node is NULL in the traversal function?
-If the root node is NULL, it means that either the tree is empty or you have reached a leaf node. In this case, the traversal function does nothing and simply returns.
Why is recursion commonly used for preorder traversal?
-Recursion is used because the preorder traversal problem is naturally recursive. For each node, you visit the root, then recursively visit the left subtree, and finally the right subtree. Recursion simplifies the implementation of this process.
How is the 'preorder' function implemented in code?
-The 'preorder' function checks if the root is NULL. If it is not, the function prints the root's data and then recursively calls itself for the left and right children of the root.
What is the structure of a tree node as mentioned in the script?
-A tree node is represented as a 'struct node', which contains data and pointers to the left and right child nodes.
What are the basic elements inside a tree node?
-Each tree node contains three elements: data (the value stored in the node), a left pointer (to the left child), and a right pointer (to the right child).
How is the preorder traversal output presented in the script?
-The preorder traversal output is presented as '4, 1, 5, 2, 6'. The presenter humorously refers to this sequence as the 'phone number' of the tree.
Why is it important to understand tree traversal in data structures?
-Tree traversal is crucial in data structures because it allows you to visit every node in a structured manner, which is essential for tasks like searching, inserting, or performing operations on each node.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
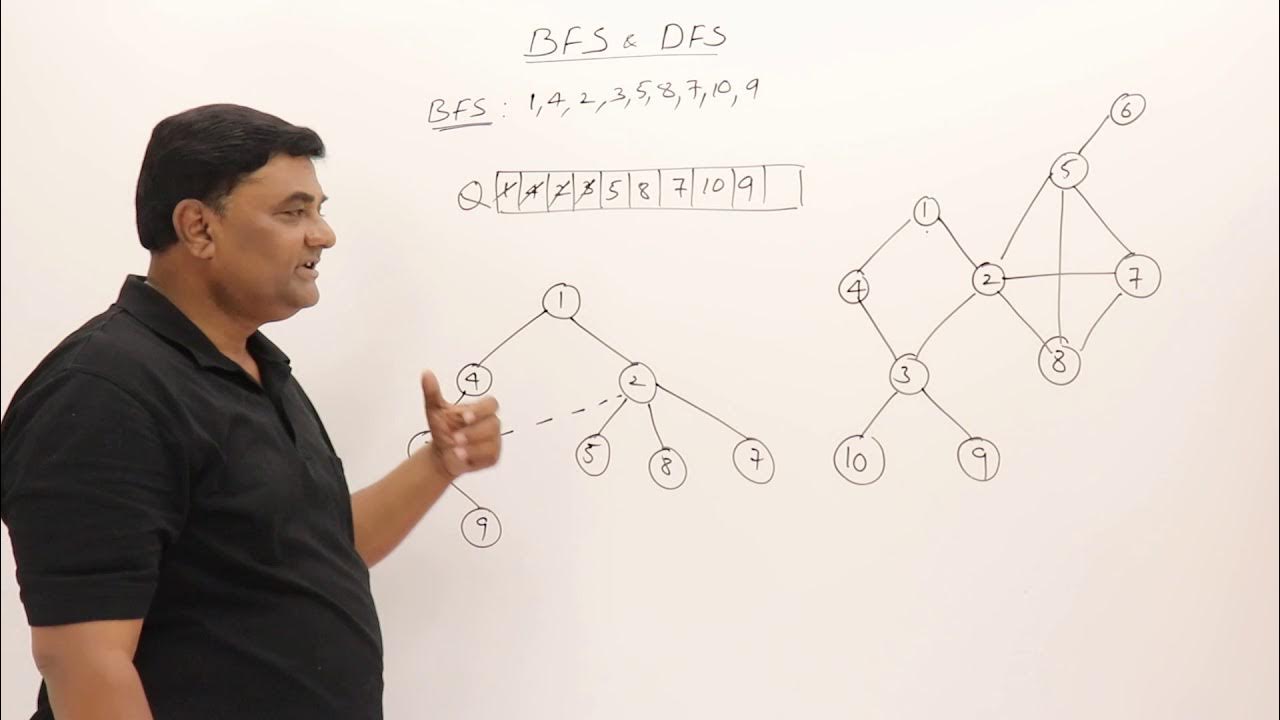
5.1 Graph Traversals - BFS & DFS -Breadth First Search and Depth First Search

AQA A’Level Reverse Polish Notation - Part 2

Depth First Search (DFS) Graph Traversal in Data Structures

AVL Trees Simply Explained

20 Data Structure Interview Questions for Freshers - TCS, Accenture, Infosys, Wipro,Cognizant,Amazon

Merkle Tree Explained Simply | Code Eater - Blockchain | Hindi
5.0 / 5 (0 votes)
