5.1 Graph Traversals - BFS & DFS -Breadth First Search and Depth First Search
Summary
TLDRThis video provides a comprehensive explanation of the two primary graph traversal methods: Breadth First Search (BFS) and Depth First Search (DFS). It starts by defining key concepts like visiting and exploring vertices and then walks through detailed examples of how each traversal method works. BFS explores vertices level by level, utilizing a queue, while DFS explores paths deeply, using a stack. The video highlights differences in their approaches, applications, and provides a clear breakdown of the data structures involved, ultimately helping viewers understand how these techniques are used to traverse graphs and trees effectively.
Takeaways
- 😀 BFS and DFS are two fundamental graph traversal methods that explore vertices in different orders.
- 😀 BFS explores vertices level by level, ensuring that all vertices at the current depth are visited before moving to the next level.
- 😀 DFS explores as deep as possible along one branch before backtracking to explore other branches.
- 😀 BFS uses a Queue data structure, while DFS uses a Stack data structure to manage the order of exploration.
- 😀 BFS is ideal for finding the shortest path in an unweighted graph, as it explores all neighbors at each level first.
- 😀 DFS is useful when you need to explore deeper nodes or solve problems like finding connected components or solving mazes.
- 😀 In BFS, you can select any vertex as the starting point, and you can visit adjacent vertices in any order at each level.
- 😀 In DFS, once a vertex is visited, you start exploring its neighbors by going deep down one path before backtracking.
- 😀 The difference between BFS and DFS can be illustrated by comparing BFS to level-order traversal of a binary tree and DFS to pre-order traversal.
- 😀 The time complexity for both BFS and DFS is O(V + E), where V is the number of vertices and E is the number of edges in the graph.
Q & A
What is the difference between Breadth-First Search (BFS) and Depth-First Search (DFS)?
-The key difference between BFS and DFS is the approach to exploration. BFS explores level by level using a queue, visiting all adjacent vertices before moving to the next vertex. DFS explores deeply along a branch using a stack, backtracking once a path is fully explored.
What are the terms 'visiting a vertex' and 'exploring a vertex' in the context of graph traversal?
-In graph traversal, 'visiting a vertex' means moving to a particular vertex, while 'exploring a vertex' means visiting all of its adjacent vertices.
What data structure is used in BFS for exploration?
-BFS uses a queue (Q) for exploration. It processes vertices in the order they are added to the queue, exploring all adjacent vertices of a vertex before moving to the next one.
What data structure is used in DFS for exploration?
-DFS uses a stack for exploration. Once a new vertex is visited, its exploration is suspended, and DFS explores deeper into the graph using the stack to backtrack when needed.
How does the traversal order in BFS compare to a binary tree?
-BFS traversal is similar to the level-order traversal in a binary tree, where vertices are explored level by level, starting from the root.
In DFS, why is exploration suspended once a new vertex is visited?
-In DFS, exploration is suspended once a new vertex is visited to allow the algorithm to explore as deeply as possible along a branch before backtracking to explore other vertices.
What is the role of the queue in BFS?
-The queue in BFS holds the vertices that are yet to be explored. Vertices are processed in the order they are added to the queue, ensuring that all adjacent vertices of a vertex are explored before moving to the next one.
What is the purpose of the stack in DFS?
-The stack in DFS helps manage the order of exploration. When a new vertex is visited, the current vertex is pushed onto the stack, and DFS continues exploring deeper into the graph. If a vertex has no unvisited neighbors, the algorithm backtracks using the stack.
What type of edges are associated with BFS and DFS?
-In BFS, the edges between vertices that are visited from the same level are called 'cross edges.' In DFS, edges that connect a vertex to a previously visited vertex are called 'back edges.'
How can BFS and DFS be performed on a tree?
-In a tree, BFS is equivalent to performing a level-order traversal, while DFS is equivalent to performing a pre-order traversal. Both algorithms explore vertices, but BFS processes them level by level, while DFS goes as deep as possible along each branch.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Depth First Search (DFS) Graph Traversal in Data Structures

Breadth First Search BFS
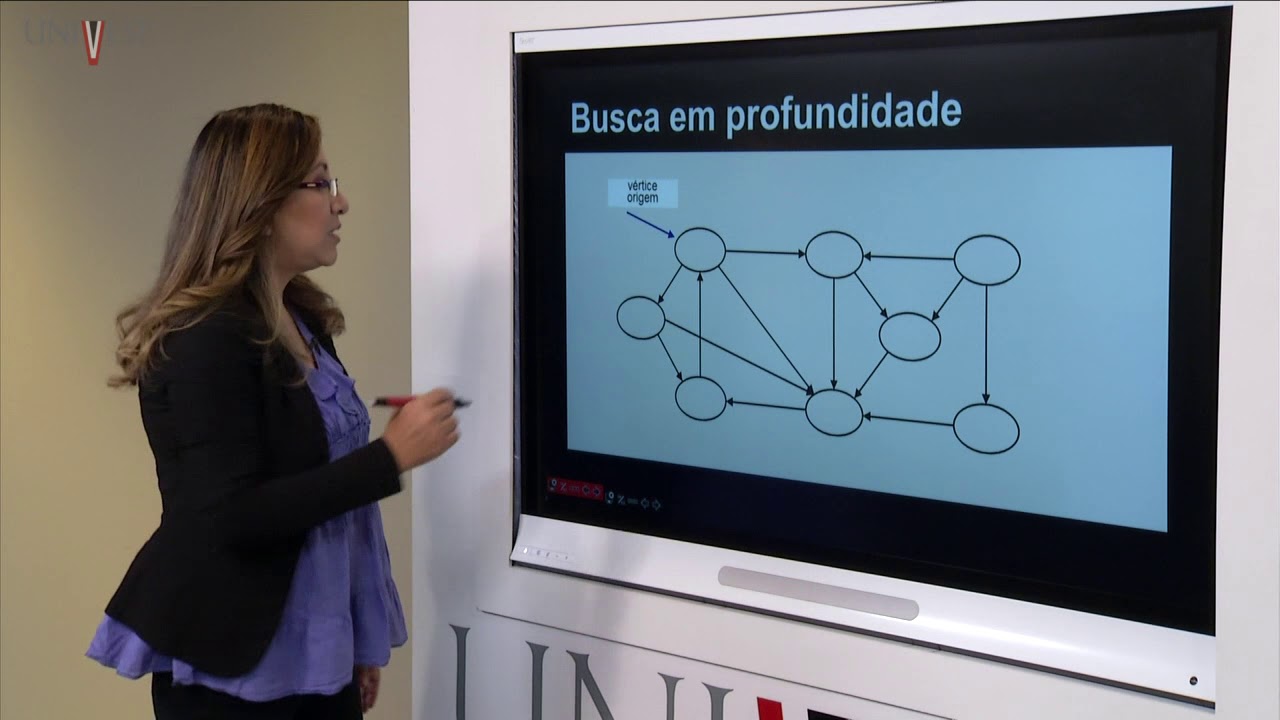
Projeto e Análise de Algoritmos - Aula 12 - Algoritmos de busca em largura e profundidade em grafos
AI - Ch03 - Uninformed search algorithms

G-5. Breadth-First Search (BFS) | C++ and Java | Traversal Technique in Graphs

Algoritma Greedy Best First Search dan A* (A star) + Contoh dan Penjelasan | Algoritma Struktur Data
5.0 / 5 (0 votes)