Grade 9 Math Q1 Ep14: Graphing a Quadratic Function
Summary
TLDRThis video is a mathematics lesson focused on quadratic functions, particularly how to rewrite them in vertex form, sketch their graphs, and identify key features such as the vertex, axis of symmetry, intercepts, and range. The instructor explains how to complete the square, calculate values, and graph the function step-by-step. Real-world examples illustrate these concepts, comparing parabolas that open upward or downward. The lesson concludes with an inspiring message about self-empowerment and support from others. Viewers are encouraged to follow along, complete tasks, and apply these skills.
Takeaways
- 📘 The quadratic function is rewritten in vertex form to better understand its properties.
- ✏️ Completing the square is a critical step in converting the quadratic equation into vertex form.
- 📝 The vertex form of the quadratic function helps identify the vertex of the parabola.
- 🔍 The function's maximum value is determined by the y-coordinate of the vertex.
- 📊 The domain of the quadratic function is all real numbers, while its range depends on the vertex's y-value.
- 📉 The parabola opens downward if the leading coefficient is negative, and upward if it is positive.
- 📌 The x-intercepts are calculated by setting the function equal to zero and solving for x.
- 📏 The axis of symmetry is described by the equation x = h, where h is the x-coordinate of the vertex.
- 🔑 A parabola's direction of opening (upward or downward) influences whether the function has a maximum or minimum value.
- 📈 The graph of the quadratic function shows the key features like vertex, intercepts, and symmetry.
Q & A
What is the process of converting the quadratic function into vertex form?
-The quadratic function is converted into vertex form by completing the square. First, factor out the coefficient of the quadratic term, then add and subtract the square of half the linear coefficient within the parentheses. The final result is a binomial squared expression.
How do you find the vertex of a parabola from the quadratic function?
-The vertex of the parabola is given by the expression (h, k) in the vertex form of a quadratic function, where h is the x-coordinate and k is the y-coordinate of the vertex. In the example given, the vertex is at (2, 5).
What does the direction of a parabola depend on in a quadratic function?
-The direction of the parabola depends on the coefficient 'a' in the quadratic function. If 'a' is negative, the parabola opens downward, and if 'a' is positive, it opens upward.
What are the domain and range of a quadratic function?
-The domain of a quadratic function is always the set of all real numbers. The range, however, depends on the vertex and the direction of the parabola. If the parabola opens downward, the range is y ≤ k, and if it opens upward, the range is y ≥ k.
How do you determine the x-intercepts of a quadratic function?
-The x-intercepts are found by setting the quadratic function equal to zero and solving for x. This can be done by solving the quadratic equation either in general form or by using the vertex form.
What is the axis of symmetry in a parabola, and how is it determined?
-The axis of symmetry is a vertical line that divides the parabola into two mirror images. It is determined by the x-coordinate of the vertex and is described by the equation x = h, where h is the x-coordinate of the vertex.
What is the significance of the y-intercept in a quadratic function?
-The y-intercept is the point where the parabola intersects the y-axis. It is found by setting x = 0 in the function. In the general form, it is equal to the constant term 'c.'
How do you know if a quadratic function has a maximum or minimum value?
-A quadratic function has a maximum value if the parabola opens downward (a < 0), and a minimum value if the parabola opens upward (a > 0). The maximum or minimum value is the y-coordinate of the vertex.
What are the steps to finding the x-intercepts using the square root method?
-To find the x-intercepts using the square root method, set the quadratic function equal to zero, apply the symmetric property, isolate the square term, take the square root of both sides, and solve for x.
What is the general form of a quadratic function and how is it related to the vertex form?
-The general form of a quadratic function is y = ax² + bx + c, while the vertex form is y = a(x - h)² + k. The vertex form is derived by completing the square from the general form, making it easier to identify the vertex.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Quadratic Functions, How to Graph Quadratic Functions, Quadratic Function Graph

Fungsi Kuadrat Bagian 1 - Matematika Wajib Kelas X m4thlab

How to Graph a Quadratic Function? Quadratic Function, Vertex, Axis of Symmetry and Parabola

Persamaan dan Fungsi Kuadrat (Materi LENGKAP)
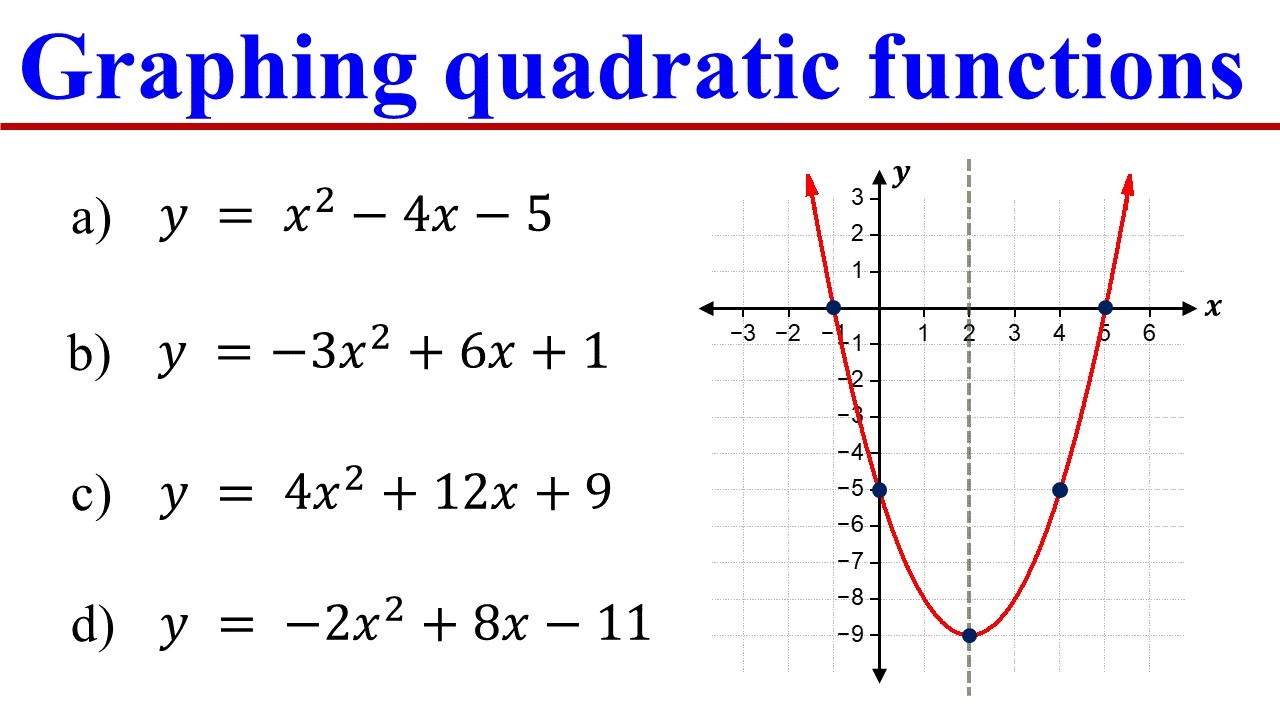
How to Graph Quadratic Functions by finding the Vertex, Axis of symmetry, X & Y intercepts
4.4 Day 1 - Graphing Parabolas in Vertex Form (Part 1)
5.0 / 5 (0 votes)
