Statics - 2D equilibrium - particle problems - example
Summary
TLDRThis tutorial explains how to solve a physics problem involving a 100 kg mass supported by three cables. The instructor draws a free body diagram, labels forces, and uses trigonometry to set up equations for forces in the x and y directions. The tutorial demonstrates solving for cable tensions using the Pythagorean theorem and algebraic manipulation, resulting in the forces in cables AB and AC.
Takeaways
- 🧑🏫 The problem involves a 100 kg mass supported by three cables (AB, AC, and AD) with specific dimensions and angles.
- 📏 AB forms a 50-degree angle with the horizontal, while AC and AD connect to the ceiling and the mass at different points.
- 📐 The vertical distance from point A to the ceiling is 3 meters, and the horizontal distance from point C to point A is 4 meters, forming a 3-4-5 right triangle.
- ✂️ A Freebody diagram is drawn, cutting through the cables to reveal forces acting on the system, including gravitational force (100 kg × 9.81 m/s²).
- 🔧 Force vectors in the cables are labeled as FA, FB, and FAC to denote forces in different directions, with vector symbols used to represent magnitude and direction.
- ➗ The force in AB is decomposed into horizontal (cosine of 50 degrees) and vertical (sine of 50 degrees) components to analyze the forces acting on the system.
- 📊 A similar triangle approach is applied to AC using the known dimensions (3 meters and 4 meters), calculating the force in the x and y directions.
- ⚖️ The equations of equilibrium for both the x and y directions (sum of forces equals zero) are used to solve for unknown forces in the cables.
- 🧮 Algebraic manipulations lead to the equation FA = 1.245 FAC, and further solving yields numerical values for the forces in the cables.
- ✅ The final calculated forces are FA = 786 Newtons and FAC = 631 Newtons, completing the solution for the problem.
Q & A
What is the total weight of the mass in Newtons?
-The mass is 100 kilograms, and the weight is calculated by multiplying the mass by the acceleration due to gravity (9.81 m/s^2), resulting in 100 kg * 9.81 m/s^2 = 981 Newtons.
What is the purpose of drawing a Free Body Diagram (FBD) in this scenario?
-A Free Body Diagram is used to visualize all the forces acting on an object, in this case, the ring supporting the mass. It helps in solving the problem by breaking down the forces into components that can be mathematically analyzed.
What are the dimensions given for the problem?
-The problem provides a 3-meter vertical drop from the ceiling to point A, and a 4-meter horizontal distance from point C to point A.
What is the angle given for cable AB?
-Cable AB makes a 50-degree angle with the horizontal.
How is the force in cable AB represented in the FBD?
-In the FBD, the force in cable AB is represented by a vector labeled as FAB or TAB, indicating that it is a vector quantity.
What is the significance of the 3-4-5 right triangle mentioned in the script?
-The 3-4-5 right triangle is used to establish the relationship between the horizontal and vertical components of the forces in the cables. It helps in determining the direction of the forces acting on the ring.
How are the forces in the x-direction calculated?
-The forces in the x-direction are calculated using the horizontal component of FAB (FAB * cos(50 degrees)) and the horizontal component of FAC (FAC * (4/5)), where 4 is the horizontal side and 5 is the hypotenuse of the 3-4-5 triangle.
What is the sum of forces equation in the x-direction?
-The sum of forces in the x-direction is set to zero: FAB * cos(50 degrees) + FAC * (4/5) = 0.
How are the forces in the y-direction calculated?
-The forces in the y-direction are calculated using the vertical component of FAB (FAB * sin(50 degrees)) and the vertical component of FAC (FAC * (3/5)), where 3 is the vertical side and 5 is the hypotenuse of the 3-4-5 triangle.
What is the sum of forces equation in the y-direction?
-The sum of forces in the y-direction is set to zero: FAB * sin(50 degrees) + FAC * (3/5) - 981 = 0.
How are the forces FAB and FAC solved for?
-The forces FAB and FAC are solved for by setting up the sum of forces equations in both the x and y directions, and then solving the system of equations.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
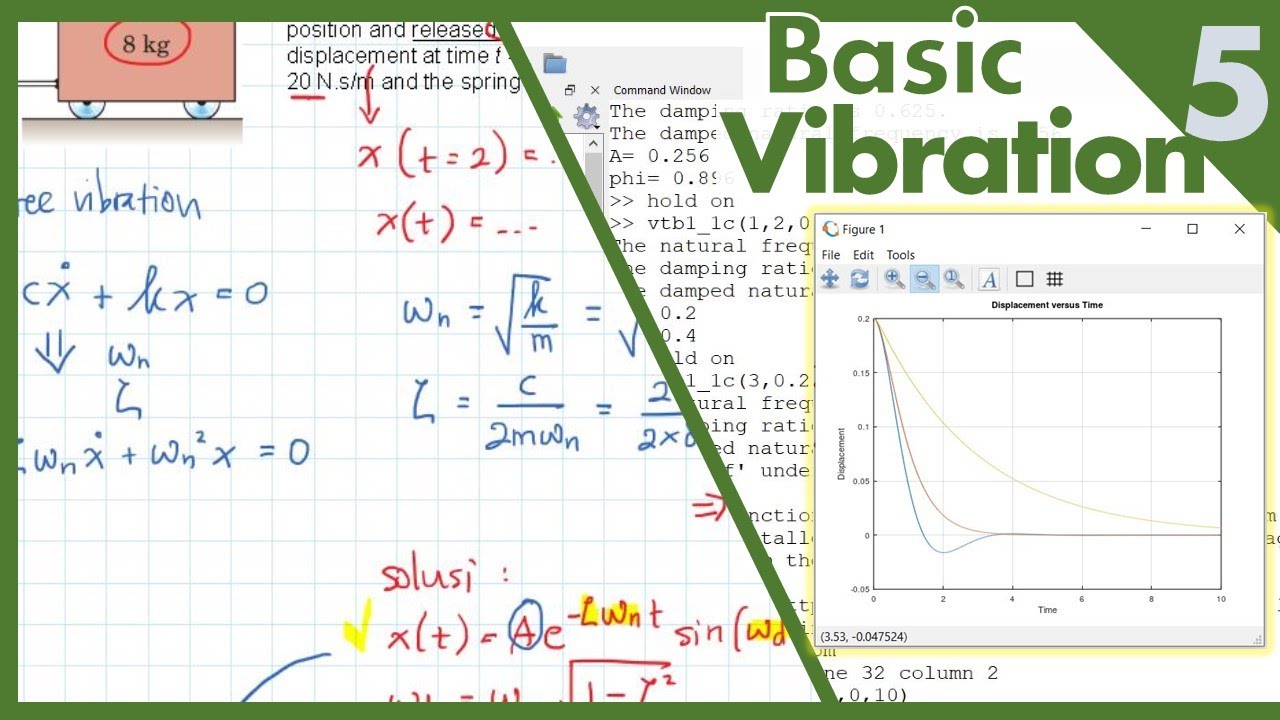
Contoh Soal Damped Free Vibration (Seri Getaran Mekanis part5)
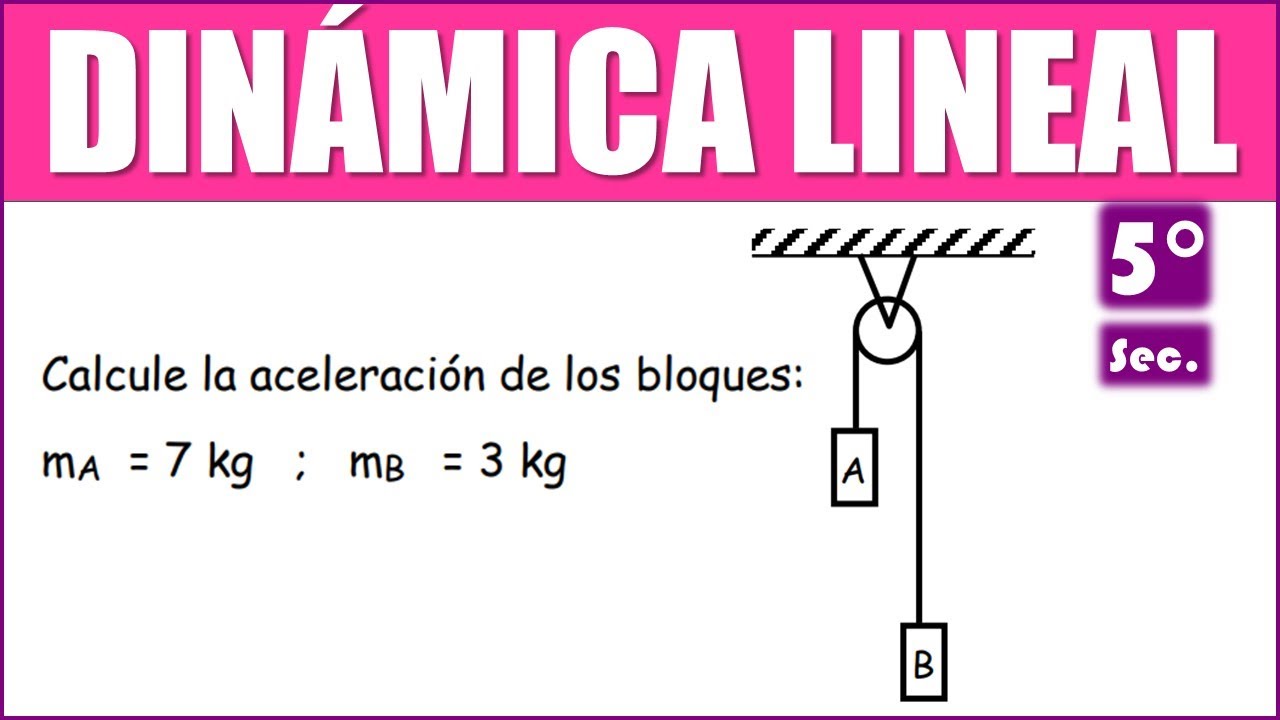
Calcule la aceleración de los bloques: mA = 7 kg ; mB = 3 kg

Sebuah benda bermassa 10 kg bergerak dengan kecepatan 20 mls: Dengan mengabaikan gaya gesek yang ...

Pertidaksamaan Linear Satu Variabel | Sistem Persamaan Linear | MANTUL | Matematika | SMP | Seg.2
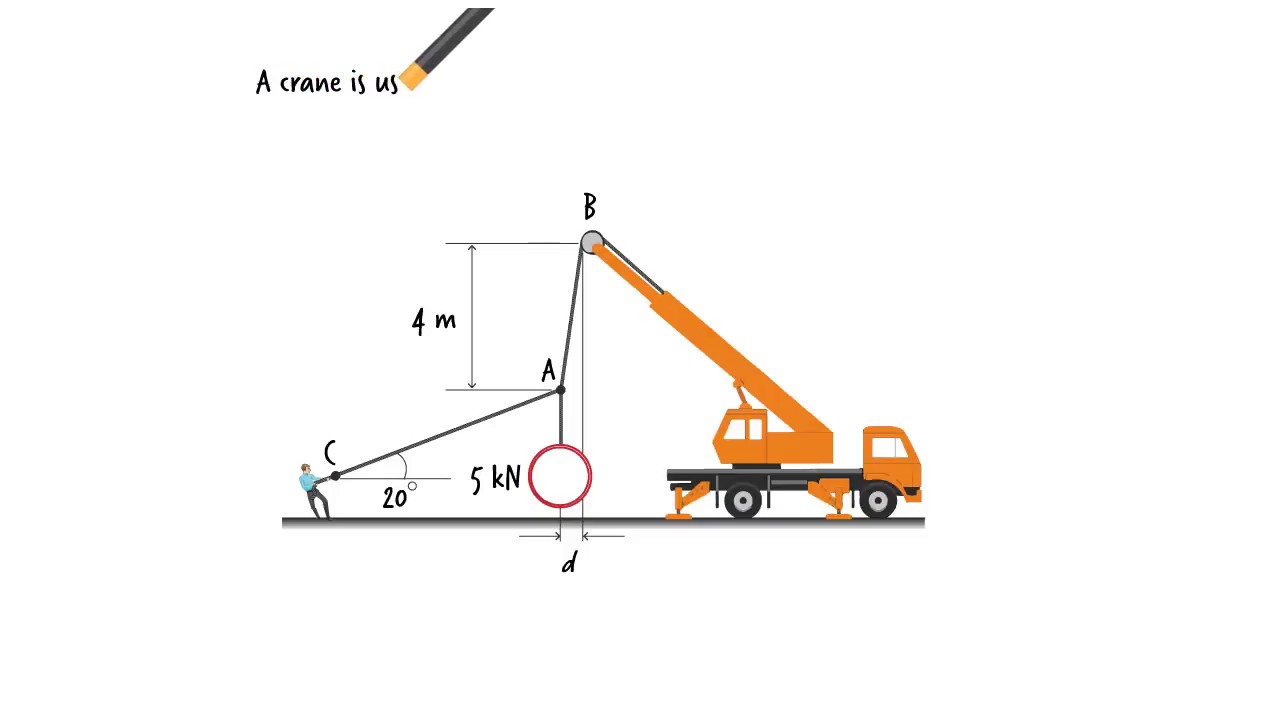
ST02: Solution for Exercise Problem 1

LEIS DE NEWTON - [FÍSICA DO ZERO]
5.0 / 5 (0 votes)
