FISIKA KUANTUM : KONSEP NORMALISASI UNTUK SUMUR POTENSIAL
Summary
TLDRThis video continues the explanation of quantum physics, focusing on the Schrodinger equation and its solutions. The presenter explains how to normalize wave functions, which is essential to ensure realistic interpretations of particle behavior. Using an example of a particle in a potential well, the normalization constant is derived, and the significance of this process is highlighted. The video also touches on statistical interpretations by Max Born and how different scenarios require different normalization constants. The presenter encourages viewers to subscribe and share for future content on various quantum physics concepts.
Takeaways
- 🎥 The video encourages viewers to subscribe and share for more content on quantum physics, including conceptual explanations and mathematical derivations.
- 🧠 The speaker introduces the Schrödinger equation and emphasizes that solving the equation is just the beginning of understanding quantum particles.
- 📐 After obtaining the wave function, it must be normalized by squaring it and integrating over all space from minus infinity to infinity, ensuring that the result equals 1.
- 🔢 The normalization constant is found by dividing 1 by the integral of the squared wave function, ensuring that the function can provide realistic physical interpretations.
- 🔍 The speaker moves to the specific case of a particle trapped in a potential well and explains the Schrödinger equation's solution for this scenario, represented by a sine function.
- 🔗 For the wave function to be realistic in the potential well case, it must be normalized by a specific constant derived through integration.
- ➕ The integration of the squared sine function yields a result that leads to a normalization constant equal to the square root of 2 divided by the length of the potential well.
- ⚖️ The conclusion is that not all solutions to the Schrödinger equation are realistic, and they must satisfy certain conditions, including statistical interpretation.
- 📊 In the potential well case, the normalization constant is the square root of 2 divided by the well's length, but this varies for different cases.
- 🔜 The speaker teases future videos where other cases and solutions of the Schrödinger equation will be discussed, urging viewers to subscribe for more content.
Q & A
What is the main topic of the video?
-The main topic of the video is quantum physics, specifically focusing on explanations and mathematical derivations related to it.
What is the purpose of normalizing the wave function?
-The purpose of normalizing the wave function is to ensure that the total probability of finding the particle in any location is equal to one.
How is the normalization of the wave function achieved?
-The normalization of the wave function is achieved by multiplying the wave function by a constant such that the integral of the square of the wave function over all space equals one.
What is the significance of the integral of the square of the wave function being equal to one?
-The integral of the square of the wave function being equal to one ensures that the probability of finding the particle somewhere in space is 100%, which is a requirement for a valid probability distribution.
What is the role of the constant 'n' in the normalization process?
-The constant 'n' is used to normalize the wave function such that when it is squared and integrated over all space, the result is one.
What does the script imply about the solutions of the Schrödinger equation?
-The script implies that not all solutions of the Schrödinger equation can be used to realistically interpret the condition of a particle; they must satisfy the statistical interpretation of Max Born.
What is a potential well in the context of quantum mechanics?
-A potential well in quantum mechanics is a region in space where the potential energy of a particle is lower than in the surrounding areas, effectively confining the particle within the well.
How does the script describe the solution to the Schrödinger equation for a potential well?
-The script describes the solution to the Schrödinger equation for a potential well as a wave function of the form sin(npx)/L, where 'n' is a constant and 'L' is the length of the well.
What is the significance of the integral involving sin^2(npx)/L in the normalization process?
-The integral involving sin^2(npx)/L is used to find the normalization constant for the wave function in a potential well, ensuring the wave function is properly normalized.
What is the final form of the normalized wave function for a particle in a potential well?
-The final form of the normalized wave function for a particle in a potential well is given by the square root of 2/L multiplied by sin(npx)/L.
What is the role of the constant 'C' in the normalized wave function?
-The constant 'C' in the normalized wave function is the normalization constant, which is the square root of 2/L, ensuring the wave function represents the particle realistically.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
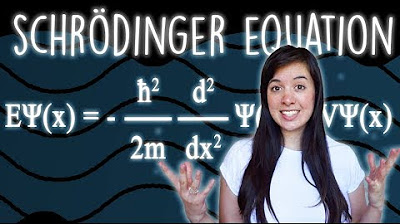
What is The Schrödinger Equation, Exactly?

The Double-Slit Experiment
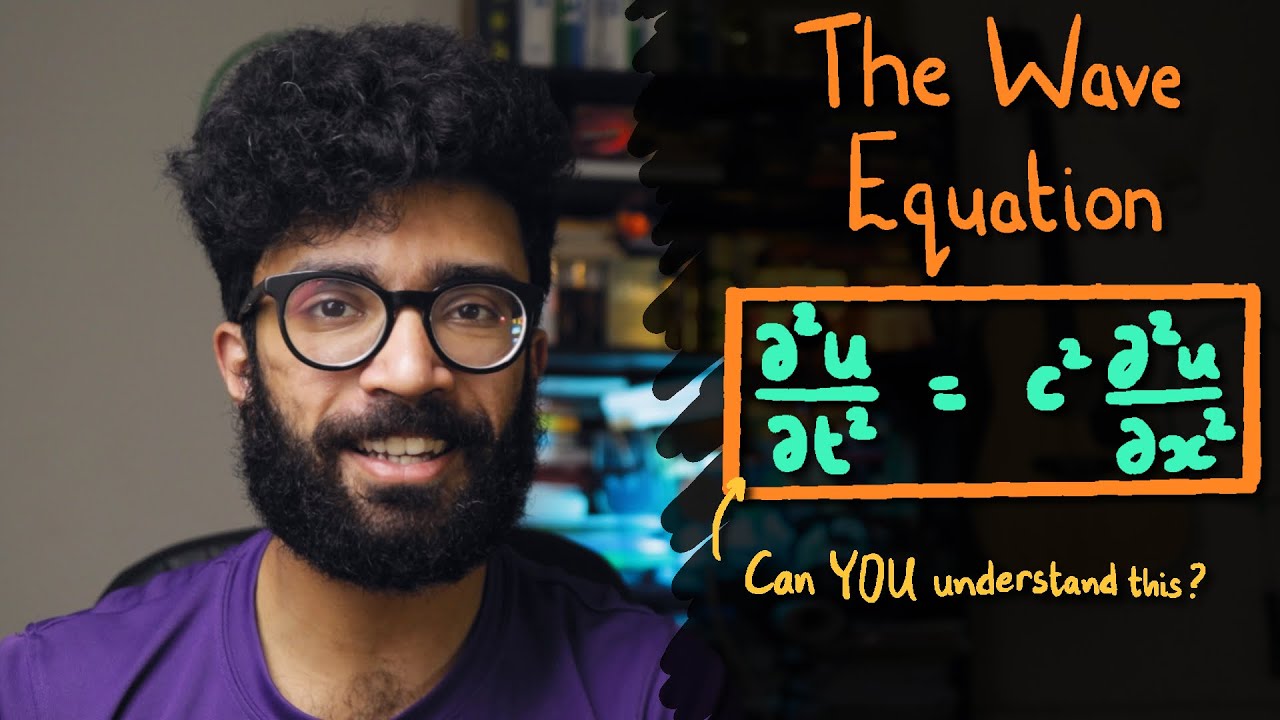
The Wave Equation for BEGINNERS | Physics Equations Made Easy

The SECOND Most Important Equation in Quantum Mechanics: Eigenvalue Equation Explained for BEGINNERS

Particles and waves: The central mystery of quantum mechanics - Chad Orzel

The Quantum Barrier Potential Part 1: Quantum Tunneling
5.0 / 5 (0 votes)
