Composición de funciones (Método fácil) (Ejemplo 2)
Summary
TLDREn este vídeo de 'Mate fácil', se explica cómo realizar la composición de funciones con dos funciones específicas: F y G. Seguidamente, se presentan las cuatro posibles composiciones: F compuesta con G, G compuesta con F, F compuesta con ella misma y G compuesta con ella misma. Se detalla el proceso paso a paso, destacando cómo sustituir y simplificar las expresiones algebraicas, y se ofrece un enlace para repasar el desarrollo de un binomio al cuadrado. Al final, se invita a los usuarios a practicar con funciones fraccionarias y a dejar sus comentarios y sugerencias.
Takeaways
- 🔢 Se discuten las cuatro posibles composiciones de funciones con F y G: F∘G, G∘F, F∘F y G∘G.
- 📝 La composición de funciones se representa con un símbolo de circulito (∘).
- 👉 Se explica que F∘G es igual a F(G(x)) y cómo se calcula sustituyendo G(x) dentro de F(x).
- 📐 Se detalla el proceso de elevar un binomio al cuadrado como parte de la composición de funciones.
- 🔗 Se ofrece un enlace a una lista de reproducción para repasar cómo elevar un binomio al cuadrado si es necesario.
- 📘 Se desarrolla el binomio (3-x)^2 para encontrar F∘G, obteniendo x^2 - 6x + 6.
- 🔄 Se calcula G∘F reemplazando F(x) en G(x), lo que resulta en -x^2 + 6.
- 🔢 Se procede a calcular F∘F, reemplazando x en F(x) por F(x), y se obtiene x^4 - 6x^2 + 9.
- 🔄 Se calcula G∘G, reemplazando x en G(x) por G(x), y se simplifica a x.
- 📚 Se menciona que el procedimiento para funciones con fracciones es similar, solo se deben recordar las operaciones con fracciones.
- 📢 Se invita a los espectadores a dar like, comentar y suscribirse para recibir más contenido similar.
Q & A
¿Qué es la composición de funciones en matemáticas?
-La composición de funciones es el proceso de aplicar una función a la salida de otra función. Se denota comúnmente con un símbolo circular y se escribe como (f ∘ g)(x) = f(g(x)).
¿Cómo se escribe la composición de funciones f ∘ g?
-La composición de funciones f ∘ g se escribe reemplazando el argumento x de la función f con la función g, es decir, f(g(x)).
¿Cuál es la función f que se menciona en el guion?
-La función f mencionada en el guion es f(x) = x^2 - 3.
¿Cuál es la función g que se menciona en el guion?
-La función g mencionada en el guion es g(x) = 3 - x.
¿Cómo se calcula f ∘ g(x) según el guion?
-Para calcular f ∘ g(x), se reemplaza x en la función f(x) = x^2 - 3 por g(x) = 3 - x, lo que resulta en f(g(x)) = (3 - x)^2 - 3.
¿Qué significa elevar un binomio al cuadrado y cómo se hace?
-Elevar un binomio al cuadrado significa multiplicar el binomio por sí mismo. Se hace aplicando la fórmula (a - b)^2 = a^2 - 2ab + b^2.
¿Cuál es el resultado de la operación (3 - x)^2 según el guion?
-Desarrollando el binomio (3 - x)^2, el resultado es 9 - 6x + x^2.
¿Cómo se calcula g ∘ f(x) según el guion?
-Para calcular g ∘ f(x), se reemplaza x en la función g(x) = 3 - x por f(x) = x^2 - 3, lo que resulta en g(f(x)) = 3 - (x^2 - 3).
¿Cuál es el resultado de la operación g(f(x)) según el guion?
-Desarrollando la operación g(f(x)) = 3 - (x^2 - 3), el resultado es -x^2 + 6.
¿Cómo se calcula f(f(x))?
-Para calcular f(f(x)), se reemplaza x en la función f(x) = x^2 - 3 por f(x) = x^2 - 3, lo que resulta en f(f(x)) = (x^2 - 3)^2 - 3.
¿Cuál es el resultado de la operación f(f(x))?
-Desarrollando la operación f(f(x)) = (x^2 - 3)^2 - 3, el resultado es x^4 - 6x^2 + 9 - 3, que simplifica a x^4 - 6x^2 + 6.
¿Cómo se calcula g(g(x))?
-Para calcular g(g(x)), se reemplaza x en la función g(x) = 3 - x por g(x) = 3 - x, lo que resulta en g(g(x)) = 3 - (3 - x).
¿Cuál es el resultado de la operación g(g(x))?
-Desarrollando la operación g(g(x)) = 3 - (3 - x), el resultado es x.
¿Qué tipo de funciones se recomienda usar para practicar la composición de funciones con fracciones?
-Se recomienda usar funciones con fracciones para practicar la composición de funciones, recordando las operaciones con fracciones de suma, resta, multiplicación y división.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
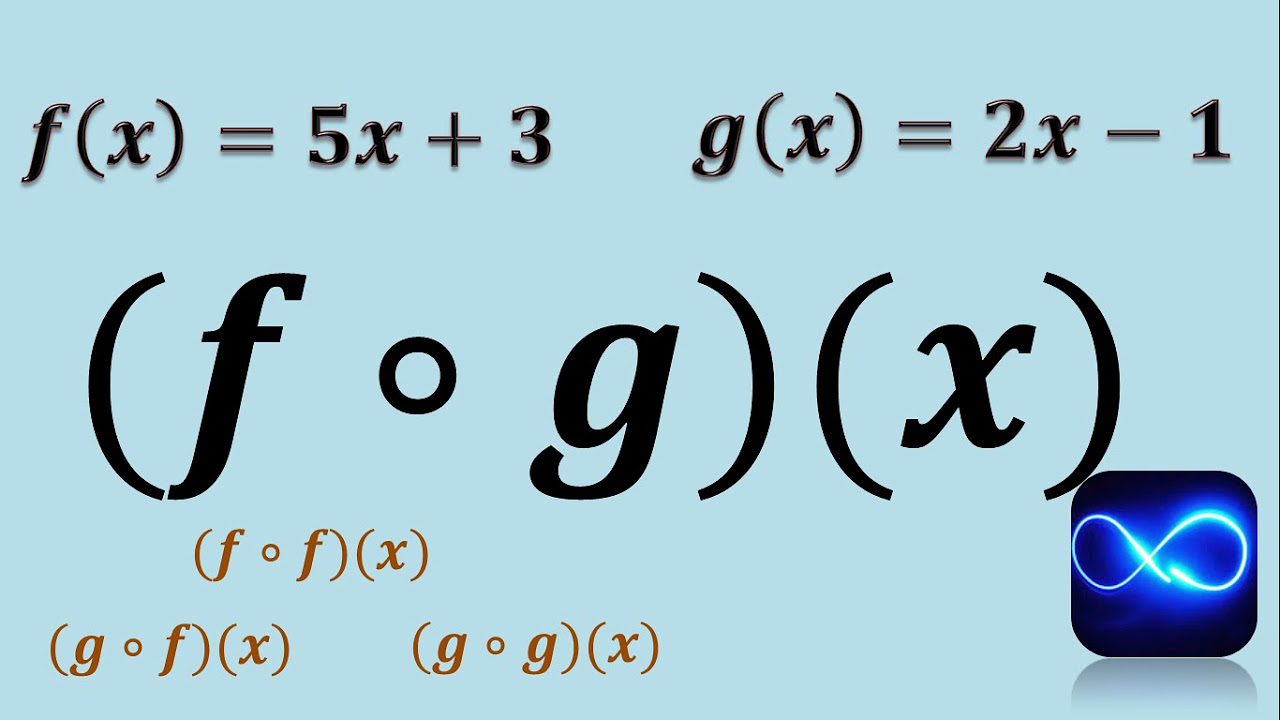
Composición de funciones (Método fácil) (Ejemplo 1)
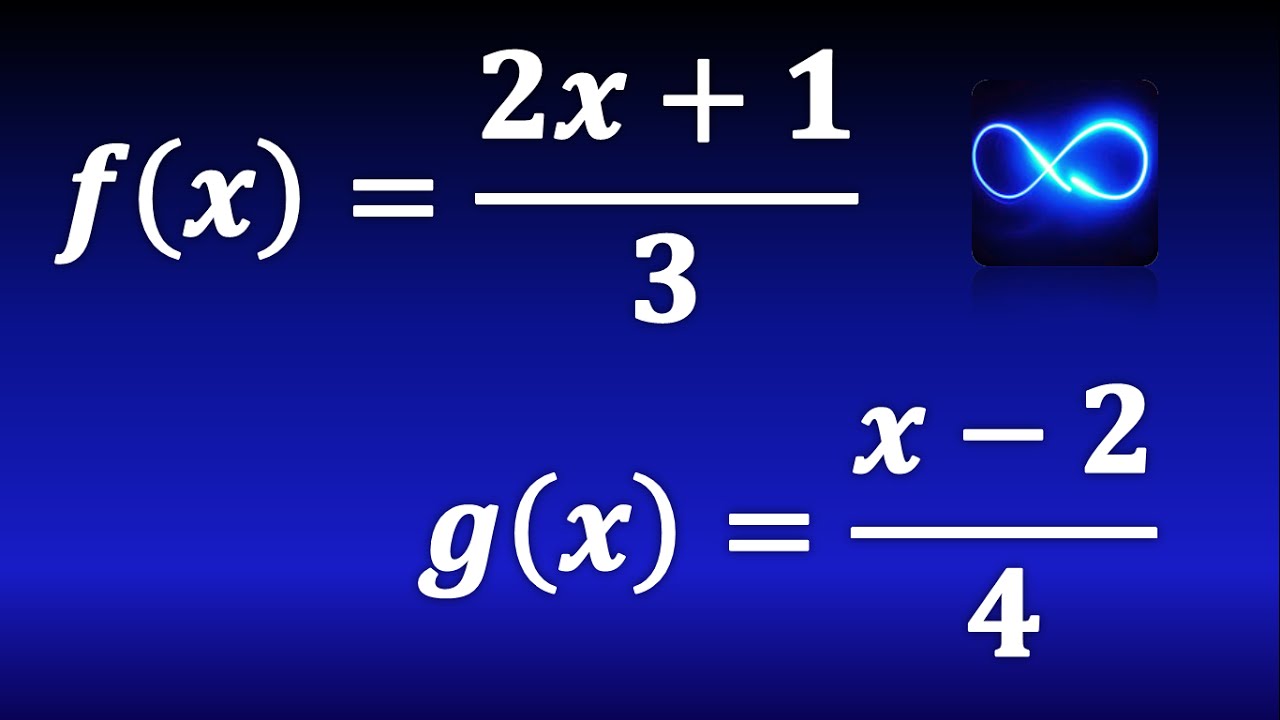
Composición de funciones (Método fácil) (Ejemplo 3)
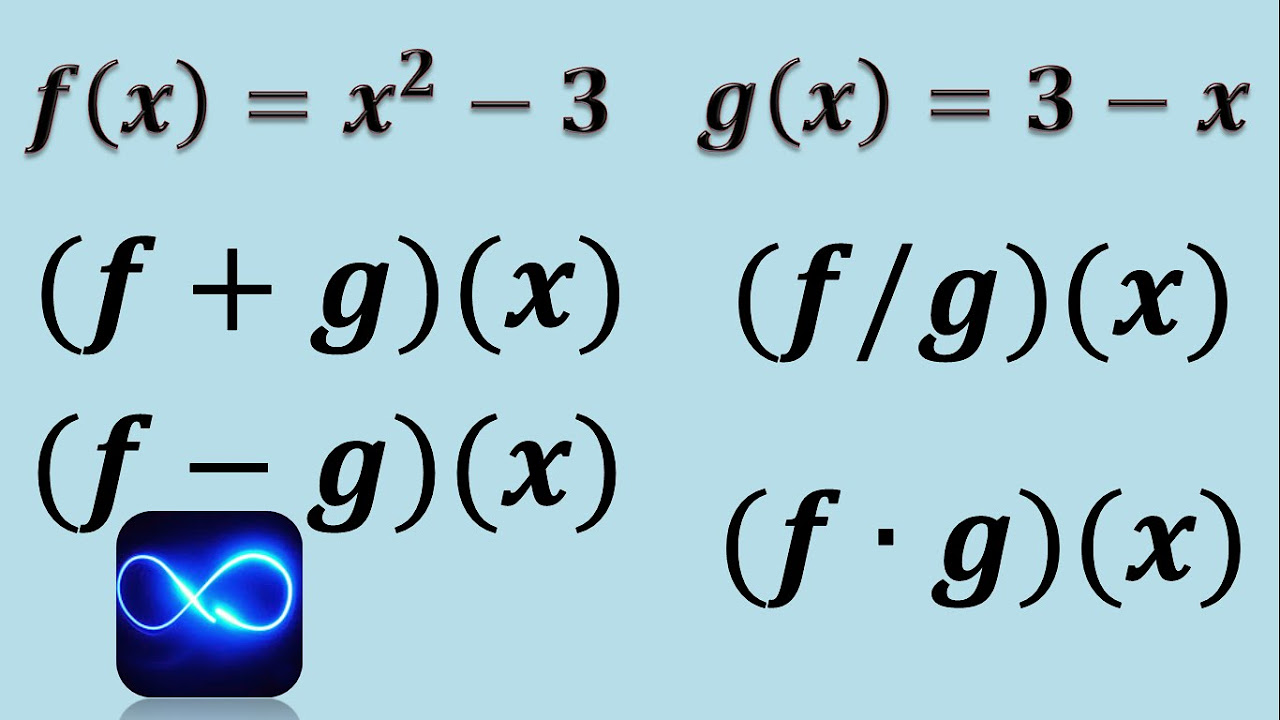
Operaciones con funciones (Suma, resta, multiplicación y división) (Ejemplo 2)

Introducción a la composición de funciones

Pensamiento matemático 3. Progresión 3a. Suma de funciones

¿Qué es la COMPOSICIÓN de FUNCIONES? | Función Compuesta | 1º bachillerato
5.0 / 5 (0 votes)