¿Qué es la COMPOSICIÓN de FUNCIONES? | Función Compuesta | 1º bachillerato
Summary
TLDREn este video, el profesor explica de manera clara y didáctica el concepto de composición de funciones para estudiantes de primero de bachillerato. A través de ejemplos prácticos, muestra cómo encadenar dos funciones f y g, destacando que la composición de funciones no es conmutativa. Utiliza analogías de la vida real, como la fabricación de un vehículo o el proceso de vestirse, para facilitar la comprensión. Además, se enfoca en la importancia de entender el concepto antes de aplicar los procedimientos matemáticos. Al final, anima a los estudiantes a practicar con más ejemplos y a seguirlo en sus redes sociales.
Takeaways
- 😀 La composición de funciones es un concepto clave en matemáticas, donde una función transforma la salida de otra función.
- 😀 Una función se puede ver como una máquina que toma una entrada (x) y la transforma en una salida (f(x)).
- 😀 El proceso de composición de funciones se puede visualizar como encadenar dos máquinas: una para transformar x en f(x) y la otra para transformar ese f(x) en g(f(x)).
- 😀 La notación de la composición de funciones se lee al revés de cómo se escribe: g ◦ f se lee como 'f compuesta con g'.
- 😀 La composición de funciones no es conmutativa, es decir, f ◦ g no es igual a g ◦ f. Esto se ejemplifica con la diferencia de ponerse la ropa en un orden correcto.
- 😀 En la práctica, la composición de funciones puede visualizarse como el encadenamiento de diferentes tareas, como en la fabricación de un vehículo.
- 😀 Para calcular la composición de dos funciones, se sustituye la salida de una función por la entrada de la otra.
- 😀 La explicación se presenta en un formato didáctico, utilizando 'cajitas' para representar visualmente la entrada y salida de cada función.
- 😀 Se calculan ejemplos prácticos de composición de funciones, como f(x) = x² - x y g(x) = 4/(x + 1), mostrando paso a paso cómo sustituir y simplificar.
- 😀 La composición de funciones también se puede aplicar a una función consigo misma, como en el caso de f ◦ f o g ◦ g, con ejemplos específicos que resultan en expresiones más complejas.
Q & A
¿Qué es la composición de funciones?
-La composición de funciones consiste en aplicar una función a la salida de otra. Es decir, se toma el resultado de una función y se lo introduce como entrada en una segunda función, generando así una nueva función.
¿Cómo se representa la composición de dos funciones f y g?
-La composición de dos funciones f y g se representa como g ∘ f, o también como g(f(x)), lo que indica que primero se aplica la función f y luego la función g sobre el resultado de f.
¿Cómo se interpreta la notación f ∘ g?
-La notación f ∘ g, o f compuesta con g, se lee de derecha a izquierda, es decir, primero se aplica la función g y luego la función f sobre el resultado de g.
¿Qué significa que la composición de funciones no es conmutativa?
-Que la composición de funciones no es conmutativa significa que el orden en que se aplican las funciones importa. Es decir, f ∘ g no es lo mismo que g ∘ f, lo cual se puede ilustrar con ejemplos prácticos.
¿Cuál es el ejemplo que ilustra la no conmutatividad de las funciones?
-Un ejemplo de la vida real es vestirse: no es lo mismo ponerse primero los calzoncillos y luego los pantalones que hacerlo al revés, donde el orden de las acciones cambia el resultado.
¿Cómo se realiza la composición de funciones en el caso de f(x) = x² - x y g(x) = 4 / (x + 1)?
-Primero, calculamos g(f(x)) al sustituir f(x) = x² - x en la función g. El resultado es g(f(x)) = 4 / (x² - x + 1). Luego, para f(g(x)), sustituimos g(x) = 4 / (x + 1) en f(x) y obtenemos una expresión más compleja.
¿Qué sucede cuando componen una función consigo misma?
-Cuando se compone una función consigo misma, por ejemplo f ∘ f, se aplica la función f a su propio resultado, lo que genera una nueva función. En el caso de f(x) = x² - x, f ∘ f(x) sería x⁴ - 2x³ + x.
¿Qué importancia tiene comprender el concepto antes de realizar los cálculos?
-Comprender el concepto detrás de la composición de funciones es fundamental, ya que esto permite realizar los cálculos de manera más clara y entender el proceso en profundidad. La intuición sobre cómo funcionan las composiciones facilita los cálculos.
¿Cómo se puede visualizar la composición de funciones de manera didáctica?
-Una forma didáctica de visualizar la composición de funciones es mediante diagramas con cajas. Cada caja representa una función, y la salida de una caja se convierte en la entrada de la siguiente. Este enfoque ayuda a entender el flujo de las transformaciones.
¿Qué implica el uso de 'cajitas' para calcular composiciones?
-El uso de 'cajitas' para calcular composiciones es una técnica didáctica que permite entender visualmente cómo se encadenan las funciones. Se representa cada función como una caja y se observa cómo la salida de una función se convierte en la entrada de la siguiente.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
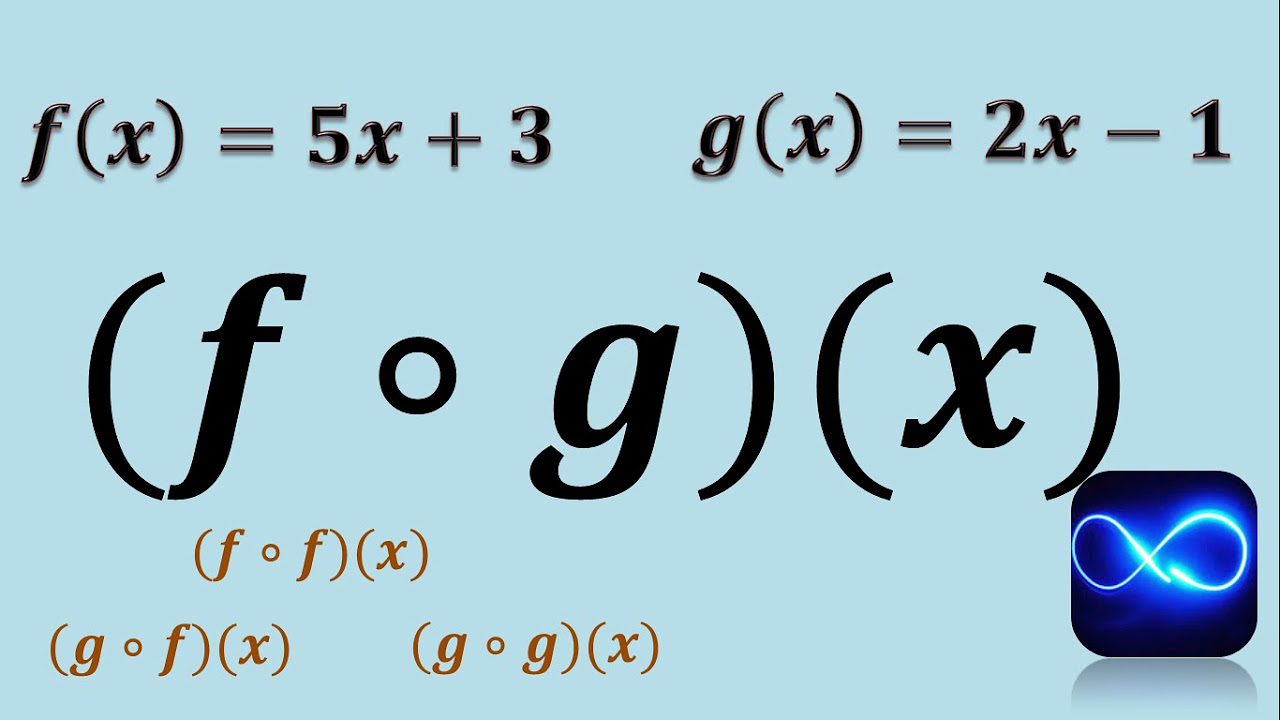
Composición de funciones (Método fácil) (Ejemplo 1)

TASA DE VARIACION INSTANTANEA

PROPORCIONALIDAD INVERSA. Explicación súper fácil!!!! 😊

Derivación Implícita | Derivada de funciones implícitas

🔴 MRU MOVIMIENTO RECTILÍNEO UNIFORME | 🚗 Explicación fórmulas y ejercicios

JERARQUÍA DE LAS OPERACIONES Superfácil - Para principiantes
5.0 / 5 (0 votes)
