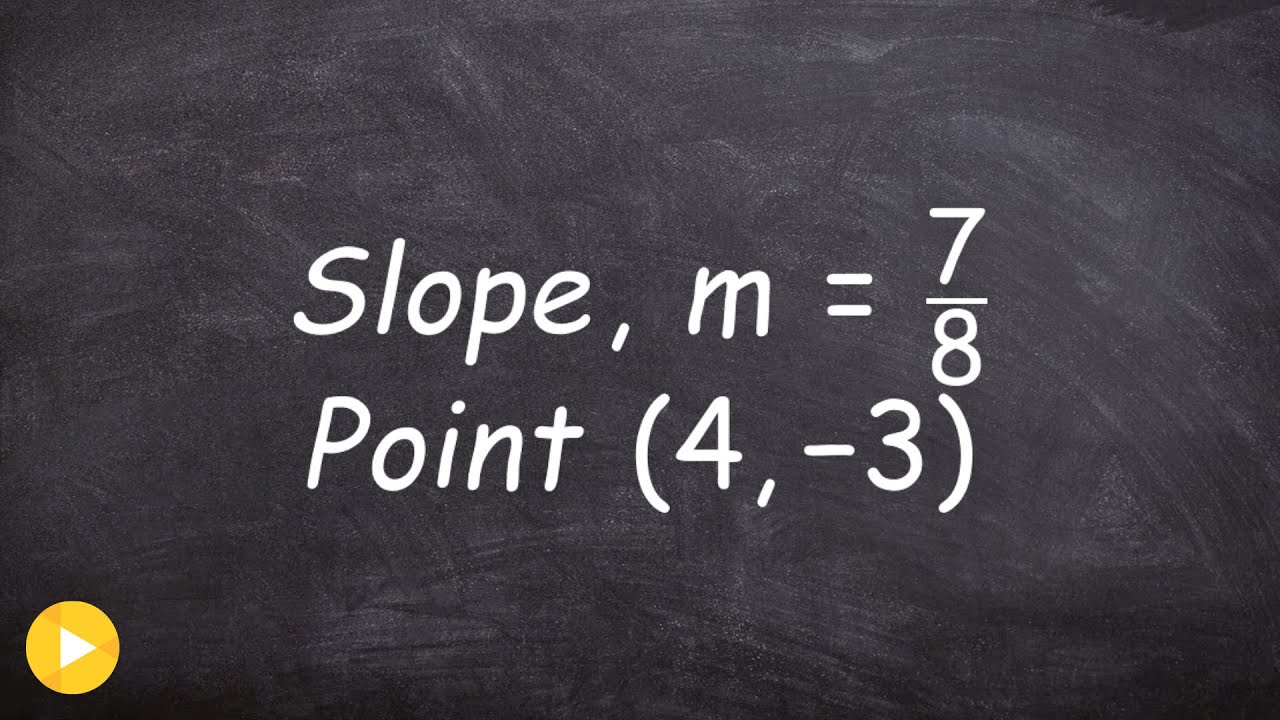Graphing a line given point and slope | Linear equations & graphs | Algebra I | Khan Academy
Summary
TLDRThe instructor guides students through the process of graphing a line with a slope of negative two that passes through the point (4, -3). The lesson emphasizes understanding the slope by demonstrating how the line can be graphed by identifying a second point based on the slope. The instructor shows two methods: increasing x by one while decreasing y by two, or decreasing x by one while increasing y by two. Both approaches yield the same line, reinforcing the concept of slope and how it affects the line's direction.
Takeaways
- 📉 The task is to graph a line with a slope of negative two, containing the point (4, -3).
- 📝 The first step is to plot the point (4, -3) on the graph by moving 4 units to the right and 3 units down from the origin.
- 🔍 To find another point on the line, we use the slope of negative two, which means as x increases by 1, y decreases by 2.
- 📐 Using the slope, another point can be found by moving from (4, -3) to (5, -5).
- 📊 Graphing two points, like (4, -3) and (5, -5), is sufficient to define the entire line.
- 🔄 An alternative method is to move in the opposite direction: if x decreases by 1, y increases by 2, due to the slope of negative two.
- 💡 Slope is the ratio of change in y to change in x (change in y / change in x).
- ↔️ Regardless of direction (positive or negative changes), the same line is created.
- ✅ The key to graphing the line is understanding how to apply the slope from a known point to find another.
- 📊 This process demonstrates two ways to find additional points for graphing using a known slope and point.
Q & A
What is the first step in graphing a line with a slope of -2 through the point (4, -3)?
-The first step is to locate the point (4, -3) on the graph. This is done by moving 4 units to the right and 3 units down from the origin.
How does the slope of -2 affect the movement of points on the graph?
-A slope of -2 means that for every increase of 1 in the x-direction, the y-coordinate decreases by 2.
What is the second point on the line if the slope is -2 and one point is (4, -3)?
-Starting from (4, -3), if x increases by 1 to 5, y decreases by 2, giving the point (5, -5) as another point on the line.
Can you move in the opposite direction to plot the line? If so, how?
-Yes, you can move in the opposite direction. If x decreases by 1, then y will increase by 2. For example, moving left from (4, -3) to (3, -1) gives another point on the line.
What does the slope of a line represent in terms of changes in x and y?
-The slope represents the ratio of the change in y to the change in x. A slope of -2 means that for every 1 unit increase in x, y decreases by 2 units.
Why is finding a second point necessary to graph a line?
-A line is determined by two points. Once two points are found, the line connecting them can be drawn, representing all possible points on that line.
What happens to y when x increases by 1 for a slope of -2?
-When x increases by 1, y decreases by 2, following the slope of -2.
How would you describe a slope of -2 in terms of rise over run?
-A slope of -2 can be described as a rise of -2 (downward) for every run of 1 (rightward).
What alternative method can be used to graph the line if moving right isn't possible?
-If space doesn't allow moving right, you can move left by decreasing x by 1 and increasing y by 2, which still follows the slope of -2.
Is the line the same whether you increase x or decrease x when plotting points based on the slope?
-Yes, the line remains the same whether you move to the right or left. The relationship between x and y dictated by the slope ensures the same line is graphed.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
5.0 / 5 (0 votes)