GCSE Physics - Velocity Time Graphs #54
Summary
TLDRThis educational video explains the concept of velocity-time graphs, which illustrate how an object's velocity changes over time. It distinguishes these from distance-time graphs and emphasizes the importance of not confusing the two. The video teaches viewers how to determine acceleration from the gradient of the curve, calculate constant velocity during flat sections, and understand increasing acceleration when the curve steepens. It also covers how to calculate the distance traveled by finding the area under the curve, using both simple geometric shapes and grid estimation for curved sections. The video concludes with an encouragement to share the educational content with others.
Takeaways
- 📊 Velocity-time graphs are used to show how an object's velocity changes over time, with velocity on the y-axis and time on the x-axis.
- ⚠️ It's crucial to distinguish between distance-time and velocity-time graphs to avoid confusion during exams.
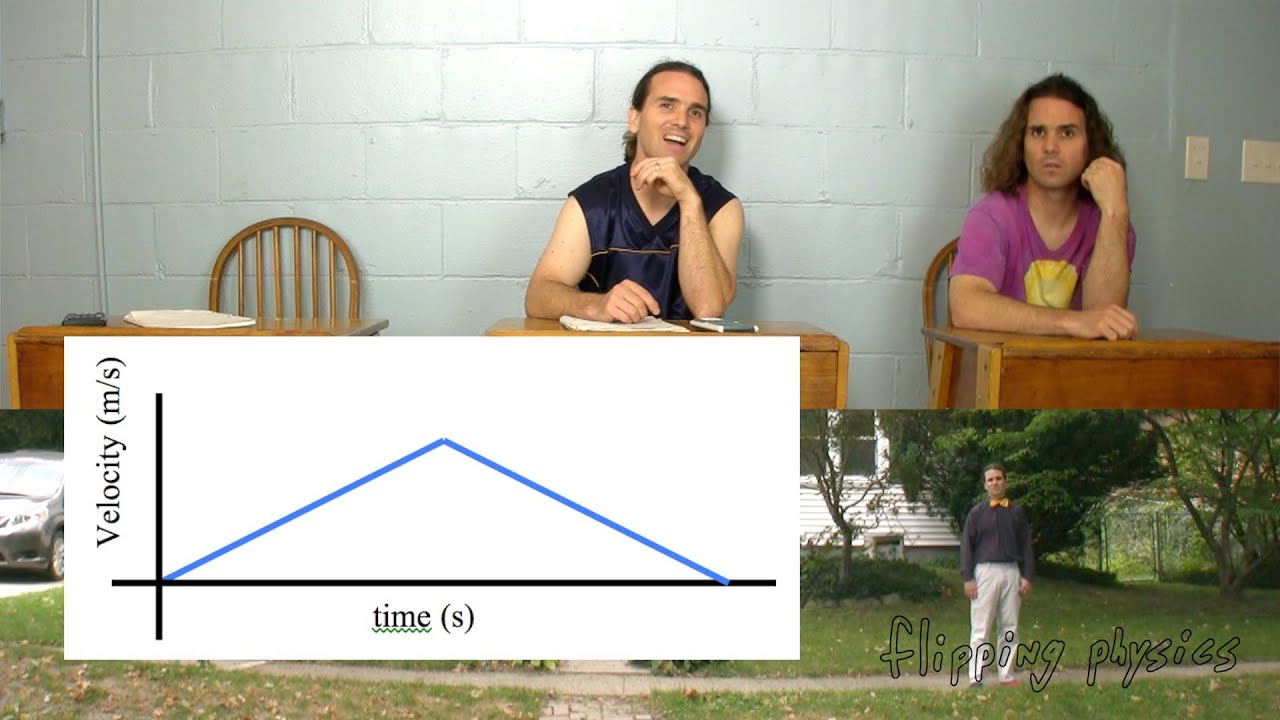
- 🔍 The gradient of the curve on a velocity-time graph represents the acceleration of the object.
- 📈 A constant positive gradient indicates constant acceleration, while a constant negative gradient indicates constant deceleration.
- 🔢 To calculate acceleration, use the formula change in velocity over change in time.
- 🏃♂️ Flat sections of the curve, with a gradient of 0, represent constant velocity as there is no acceleration or deceleration.
- 📋 To find the velocity during constant velocity periods, simply read the y-axis value.
- 📉 If the curve becomes steeper, it signifies an increasing rate of acceleration.
- 📏 The distance traveled can be found by calculating the area under the curve, which can be done by dividing the area into simpler shapes like triangles and rectangles.
- 📐 For curved sections, estimate the area by counting the number of squares under the curve on a grid, with each square representing a unit of distance.
- 💡 Remember, even though the area is calculated in square units, the result for distance traveled is expressed in linear units (meters).
Q & A
What are the key differences between distance-time graphs and velocity-time graphs?
-Distance-time graphs show how the distance of an object varies over time, while velocity-time graphs show how an object's velocity changes over time. The key difference is the variable on the y-axis: distance for distance-time graphs and velocity for velocity-time graphs.
Why is it important to distinguish between velocity-time graphs and distance-time graphs during exams?
-It is important because the two graphs look similar, and confusing them can lead to incorrect interpretations and calculations. The axes represent different physical quantities, and understanding which graph you are looking at is crucial for applying the correct formulas and concepts.
What does the gradient of a velocity-time graph represent?
-The gradient of a velocity-time graph represents the acceleration of the object. If the gradient is constant, it indicates a constant acceleration or deceleration depending on whether it's positive or negative.
How do you calculate acceleration from a velocity-time graph?
-You calculate acceleration by finding the change in velocity over the change in time, which is the gradient of the curve at any given point on the graph.
What does a flat section of the curve on a velocity-time graph indicate about the object's motion?
-A flat section of the curve indicates that the object's velocity is constant, as there is no change in velocity over time, which means the object is not accelerating or decelerating.
How can you determine the velocity of an object during a period of constant velocity from a velocity-time graph?
-During a period of constant velocity, you can determine the velocity of the object by looking at the y-axis value where the curve is flat.
What does an increasing gradient on a velocity-time graph signify?
-An increasing gradient on a velocity-time graph signifies that the rate of acceleration is increasing.
How can you find the distance traveled by an object from a velocity-time graph?
-You can find the distance traveled by calculating the area under the curve of the velocity-time graph. For straight sections, you can use geometric shapes like triangles or rectangles to find the area.
Why do we not convert the area under the curve on a velocity-time graph to meters squared when calculating distance?
-When calculating distance from the area under the curve on a velocity-time graph, we leave the answer in meters because we are interested in the total distance traveled, not the area in a two-dimensional sense.
How can you estimate the distance traveled during a period represented by a curved section on a velocity-time graph?
-You can estimate the distance traveled during a curved section by counting the number of squares under that section of the graph, where each square represents a unit of distance, and combining partial squares to approximate full squares.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahora5.0 / 5 (0 votes)